【算法专题】快慢指针的应用

Alfly 收录于笔记和算法笔记

2023-12-05 约 2700 字预计阅读 6 分钟

推荐快慢指针-讲解视频

找链表中心

实现方法

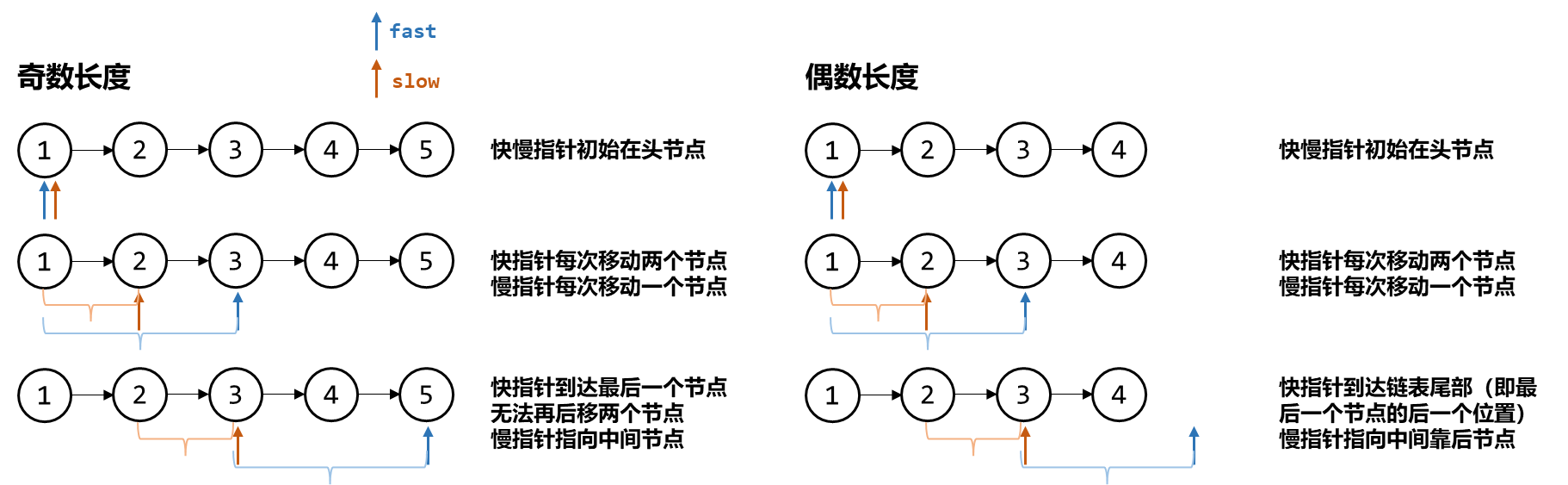
设置快指针 fast 每次移动 2 步，满指针 slow 每次移动 1 步，当 fast 移动到链表末尾（为空或为最后一个节点）时，slow 指向的就是中间节点。

在实现上有个细节，即快指针的起始位置：

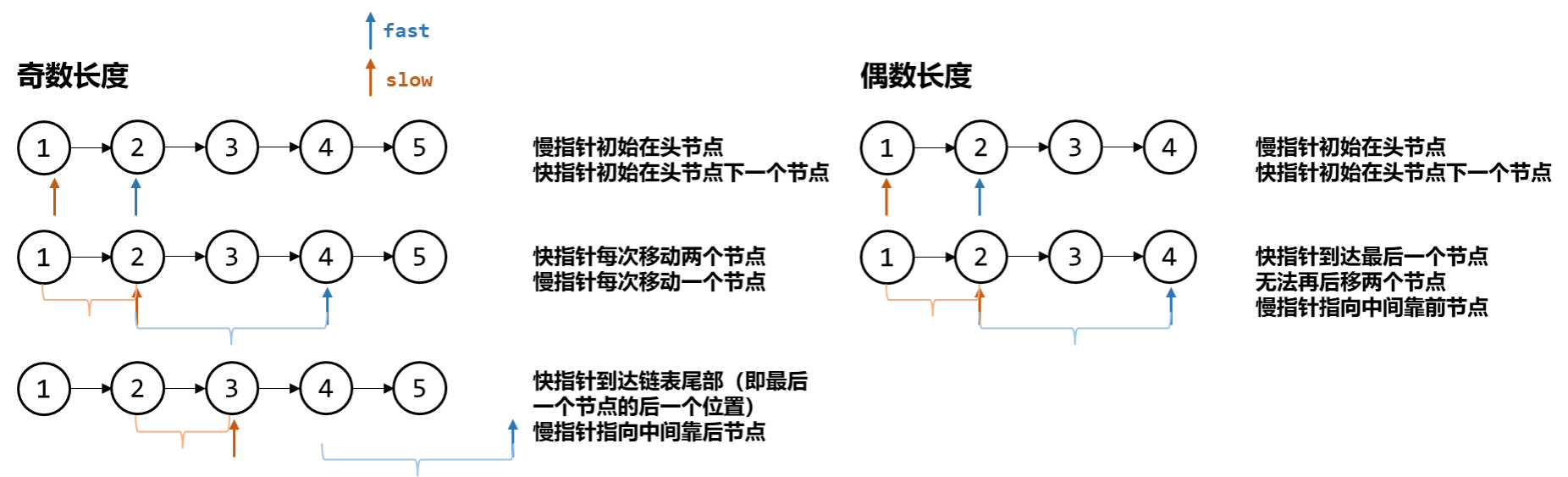
快慢指针都在头节点，当链表长度为偶数，慢指针最终指向中间靠后的节点
慢指针从头节点出发，快指针从头节点的下一个节点出发，慢指针指向中间靠前的那个节点

当链表长度为奇数时，无论那种情况，慢指针都是指向中间节点

1
2
3
4
5
6
7
8


ListNode* getMid(ListNode *head) {
	ListNode *slow = head, *fast = head;
	while (fast && fast->next) {
		slow = slow->next;
		fast = fast->next->next;
	}
	return slow;
}

如果想要指向中间靠前的那个节点（长度为偶数时），让慢指针从头节点出发，快指针从头节点的下一个节点出发。

1
2
3
4
5
6
7
8
9


ListNode* getMid(ListNode *head) {
	if (!head) return head;
	ListNode *slow = head, *fast = head->next;
	while (fast && fast->next) {
		slow = slow->next;
		fast = fast->next->next;
	}
	return slow;
}

应用-链表的归并排序

Leetcode-148. 排序链表 | Code

找到链表的中心后，分割链表，进行递归

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44


class Solution {
public:
    // 获取以 head 为头节点的链表中间节点
    // fast 从 head->next 出发，则当链表长度为偶时返回 slow 为中间靠左的节点
    ListNode* getMid(ListNode *head) {
        if (!head) return head;
        ListNode *slow = head, *fast = head->next;
        while (fast && fast->next) {
            slow = slow->next;
            fast = fast->next->next;
        }
        return slow;
    }
    ListNode *merge(ListNode *l1, ListNode *l2) {
        ListNode *h = new ListNode(), *p = h;
        while (l1 && l2) {
            if (l1->val < l2->val) {
                p->next = l1;
                l1 = l1->next;
            } else {
                p->next = l2;
                l2 = l2->next;
            }
            p = p->next;
        }
        p->next = l1 ? l1 : l2;
        return h->next;
    }
    ListNode* sortList(ListNode* head) {
        if (!head || !head->next) return head;  // 递归出口

        // 二分
        ListNode *mid = getMid(head);
        ListNode *t = mid->next;
        mid->next = nullptr;  // 分割

        // 递归
        ListNode *l1 = sortList(head);
        ListNode *l2 = sortList(t);

        // 合并
        return merge(l1, l2);
    }
};

应用-回文链表

Leetcode-234. 回文链表 | Code

方法一：找到链表的中心后，将链表的后半部分反转

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44


class Solution {
public:
    bool isPalindrome(ListNode* head) {
        if (head == nullptr) return true;

        // 找到中间节点
        ListNode *p = head, *q = head;
        while (q->next && q->next->next) {
            p = p->next;
            q = q->next->next;
        }
        ListNode *mid = p;  // 2n->n, 2n+1->n+1

        // 反转后半部分链表
        ListNode *right_head = reverseList(mid->next);

        // 比较
        ListNode *l = head, *r = right_head;
        bool res = true;
        while (l && r) {
            if (l->val != r->val) {
                res = false;
                break;
            }
            l = l->next;
            r = r->next;
        }

        // 还原链表
        mid->next = reverseList(right_head);
        return res;
    }

    ListNode* reverseList(ListNode* head) {
        ListNode *pre = nullptr, *cur = head;
        while (cur) {
            ListNode *next_cur = cur->next;
            cur->next = pre;
            pre = cur;
            cur = next_cur;
        }
        return pre; // cur = null
    }
};

方法二：找中心的同时反转链表

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


class Solution {
public:
    bool isPalindrome(ListNode* head) {
        if (head == nullptr) return true;

        // 找到中间节点
        ListNode *p = head, *q = head;  // 快慢指针
        ListNode *cur = head;           // 当前翻转的节点
        ListNode *h = new ListNode();   // 翻转后的头节点(空节点)
        while (q && q->next) {
            p = p->next;
            q = q->next->next;
            // 翻转
            cur->next = h->next;
            h->next = cur;
            cur = p;
        }
        // 链表长度为奇数，p 跳过中心节点
        if (q != NULL) p = p->next;

        // 比较
        h = h->next;
        while (h && p) {
            if (h->val != p->val) return false;
            h = h->next;
            p = p->next;
        }
        return true;
    }
};

判断链表有环

基本原理

设置快指针 fast 每次移动 2 步，满指针 slow 每次移动 1 步

链表无环：

快指针会率先到达终点（先访问到 null）
慢指针永远不会与快指针相遇

链表有环：

慢指针可以与快指针相遇

Leetcode-141. 环形链表 | 遍历法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode *slow = head, *fast = head;
        while (fast && fast->next) {  // 含环则不会有 NULL, 以 fast 为判断标准
            slow = slow->next;        // slow pointer
            fast = fast->next->next;  // fast pointer
            if (slow == fast) {
                return true;
            }
        }
        return false;
    }
};

指针速度对结果的影响

当慢指针为 1 时，快指针为 2 为什么正确呢，是不是只能为 2 呢？快指针与慢指针的关系如何呢？

假设 slow 与 fast 在 t 时刻相遇，此时 fast 比 slow 多走完整 n 圈 $(n >= 1)$，L 为环的长度。

\begin{align*} (v_2 - v_1) * t &= n * L \\ => t &= \frac {n * L} {v_2 - v_1} \end{align*}

当上式成立则达成相遇条件；$v1 = 1, v2 = 2$ 时，n 可取最小值 1，即多跑一圈即可相遇。

速度间隔为环长度的整数倍时，快慢指针会在环内某点相遇后一直保持同步

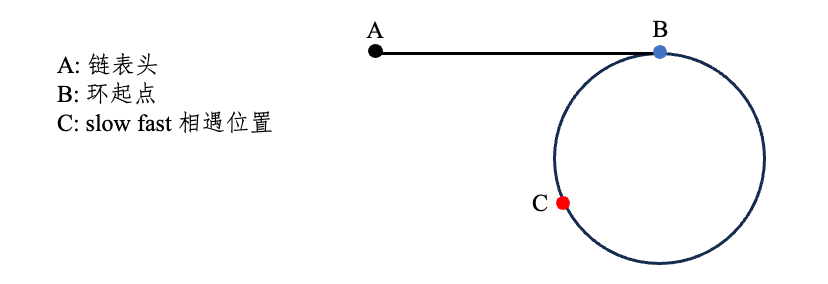
找环的起点

fast 与 slow 在 C 点相遇时，fast 走的距离是 slow 的 2 倍。这里假设 fast 走过完整 m 圈，slow 走过完整 n 圈，则有：

\begin{align*} ac + m * L &= 2 * (ac + n * L) \\ => (m - n) * L &= ac \end{align*}

若通过 $V_{slow} = 1, V_{fast} = 2$ 完成环的判断，fast 和 slow 均在环内时，fast 每次追一步。由于追的距离小于环的长度，所以相遇时 slow 没有完整走完一圈，fast 比 slow 多走一圈，即 $m = 1, n = 0$。

\begin{align*} &L = ac \\ &=> bc + cb = ab + bc \\ &=> cb = ab \end{align*}

设置两个同速指针 $V_p = V_q = 1$，一个位于链表头，另一个位于此前 slow/fast 的相遇位置，它们会在环的起点相遇。

Leetcode-142. 环形链表 II | Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        // 判断环
        ListNode *p = head, *q = head;
        while (q && q->next) {    // Vp = 1 Vq = 2
            p = p->next;
            q = q->next->next;
            if (p == q) break;
        }
        if (q == NULL || q->next == NULL) return NULL;  // 无环
        // 环的起点
        p = head;
        while (p != q) {
            p = p->next;
            q = q->next;
        }
        return q;
    }
};

也可以通过朴素遍历的方式：找到环后，在环内遍历求出环长 L，再双指针求链表倒数第 L 个点

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        // 判断环
        ListNode *p = head, *q = head;
        while (q && q->next) {      // Vp = 1 Vq = 2
            p = p->next;
            q = q->next->next;
            if (p == q) break;
        }
        if (q == NULL || q->next == NULL) return NULL;  // 无环
        // 环的长度
        ListNode *t = p->next;
        int len = 1;
        while (t != p) {
            t = t->next;
            len++;
        }
        // 环的起点（链表倒数第 len 的节点）
        ListNode *x = head, *y = head;
        while (len--) y = y->next;    // 先多走一个环的长度
        while (x != y) {
            x = x->next;
            y = y->next;
        }
        return x;
    }
};

其他变式

判断环

Leetcode-202. 快乐数 | Code

int 类型最大值 $2,147,483,647$，平方和最大的数是 $1,999,999,999$，平方和为 $1 + 81*9 = 724$。可知任何数的平方和都在1到724之间，724次循环之内一定有重复的，一定不会出现死循环。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


class Solution {
public:
    int square_sum(int n) {
        int sum = 0;
        while (n) {
            sum += (n % 10) * (n % 10);
            n /= 10;
        }
        return sum;
    }
    bool isHappy(int n) {
        int p = n, q = square_sum(n);
        while (p != q) {
            p = square_sum(p);
            q = square_sum(square_sum(q));
        }
        return p == 1;
    }
};

找环起点

Leetcode-287. 寻找重复数 | Code

给定一个包含 n + 1 个整数的数组 nums，其数字都在 [1, n] 范围内（包括 1 和 n）。假设 nums 只有一个重复的整数，返回这个重复的数。

我们对 $nums$ 数组建图，每个位置 i 连一条 i -> nums[i] 的边，得到一个链表。由于存在重复的数字 target，因此 target 一定有两条指向它的边，因此整张图一定存在环。

[1,3,4,2] 可建成链表：0->1->3->2->4->null
[1,3,4,2,2] 可建成链表：0->1->3->2->4->2
[3,2,3,4,2] 可建成链表：0->3->4->2->3

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        // i -> nums[i] 的链表结构
        int n = nums.size();
        int p = 0, q = 0;
        while (q < n && nums[q] < n) {
            p = nums[p];
            q = nums[nums[q]];
            if (p == q) break;
        }
        p = 0;
        while (p < n && q < n) {
            p = nums[p];
            q = nums[q];
            if (p == q) break;
        }
        return p;
    }
};

while 判断的不同写法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        // i -> nums[i] 的链表结构
        // int p = 0, q = nums[0]; // 可能超时错误，因为不是从起点 0 出发同步到达，后续找环起点要从链表头开始
        int p = nums[0], q = nums[nums[0]];  // 0->p, 0->->q 为了进入 while 循环初始设置值不等
        while (p != q) {
            p = nums[p];
            q = nums[nums[q]];
        }
        p = 0;
        while (p != q) {
            p = nums[p];
            q = nums[q];
        }
        return p;
    }
};

Reference

画图小匠：链表的综合操作【图解】

收录于合集・算法笔记 14

【算法专题】组合与排列【算法专题】Rand 概率生成