【算法专题】铺瓷砖

铺瓷砖一般场景是使用一块或多块形状不同的瓷砖，对墙面进行无缝平铺，计算指定墙面下有多少种铺法或消耗瓷砖最少的铺法。

方案数

$2 * n$ 墙面

A 砖 $2 * 1$：$dp[i] = dp[i - 1] + dp[i - 2]$

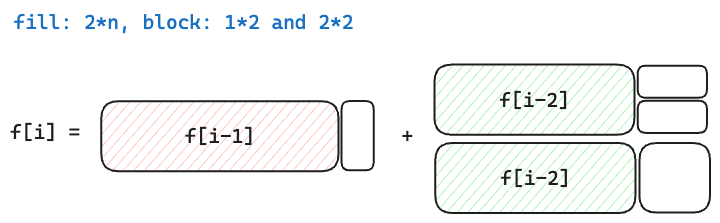
A 砖 $2 * 1$，B 砖 $2 * 2$：$dp[i] = dp[i - 1] + 2 * dp[i - 2]$

A 砖 $2 * 1$，B 砖 $2 * 3$：$dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]$

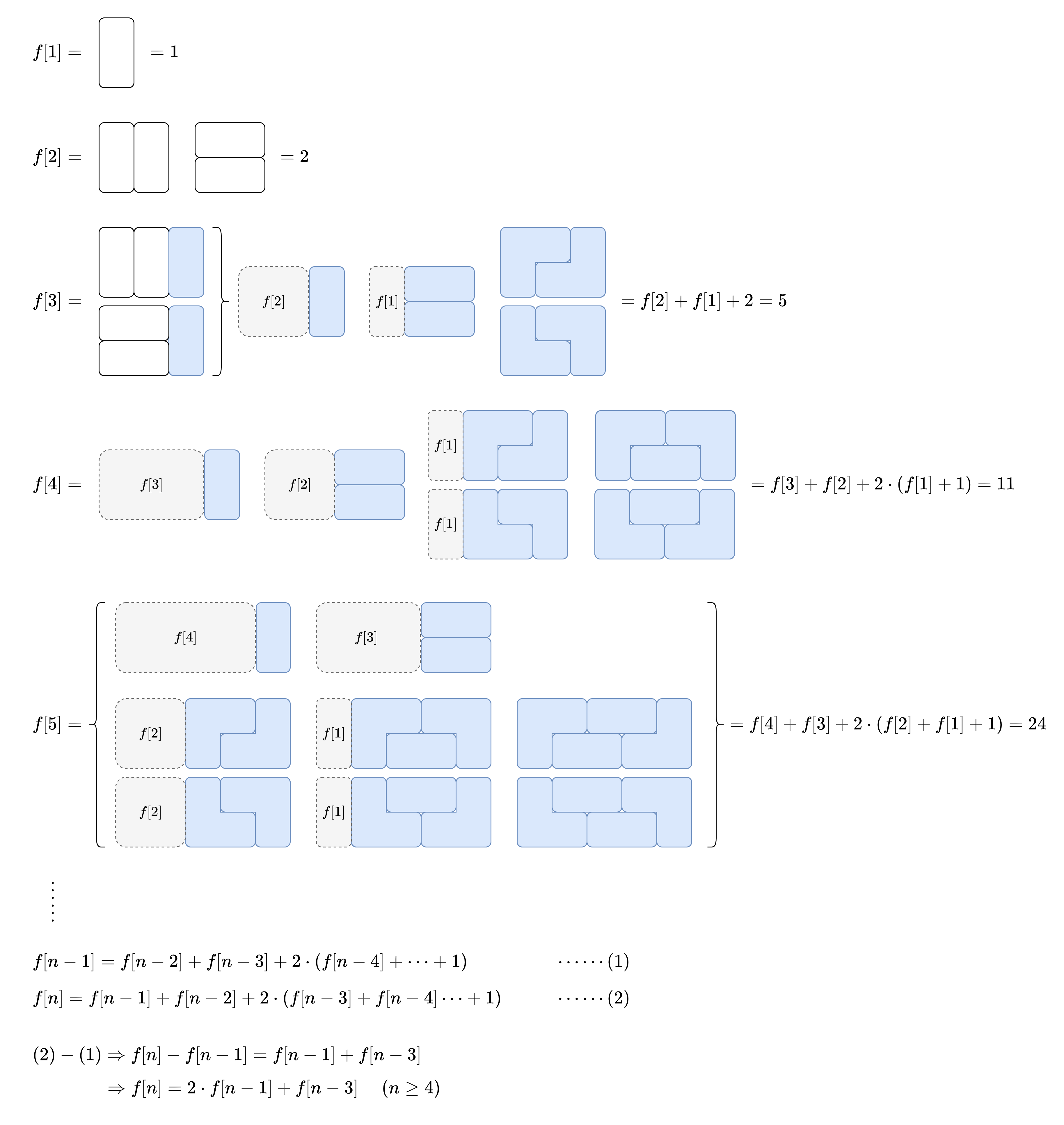
A 砖 $2 * 1$，B 砖 L 型（三块小砖组成）：$dp[i] = 2 * dp[i - 1] + dp[i - 3]$

leetcode - 790. 多米诺和托米诺平铺

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

class Solution {
public:
    const int M = 1e9+7;
    int numTilings(int n) {
        long f[1001];
        f[1] = 1, f[2] = 2, f[3] = 5;
        if (n <= 3) return f[n];
        for (int i = 4; i <= 1000; i++) f[i] = (2 * f[i - 1] + f[i - 3]) % M;
        return f[n];
    }
};

$3 * n$ 墙面

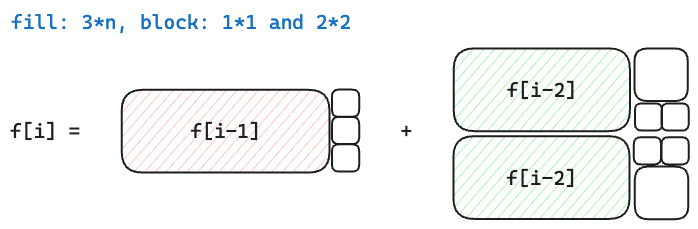
A 砖 $1 * 1$，B 砖 $2 * 2$：$dp[i] = dp[i - 1] + 2 * dp[i - 2]$

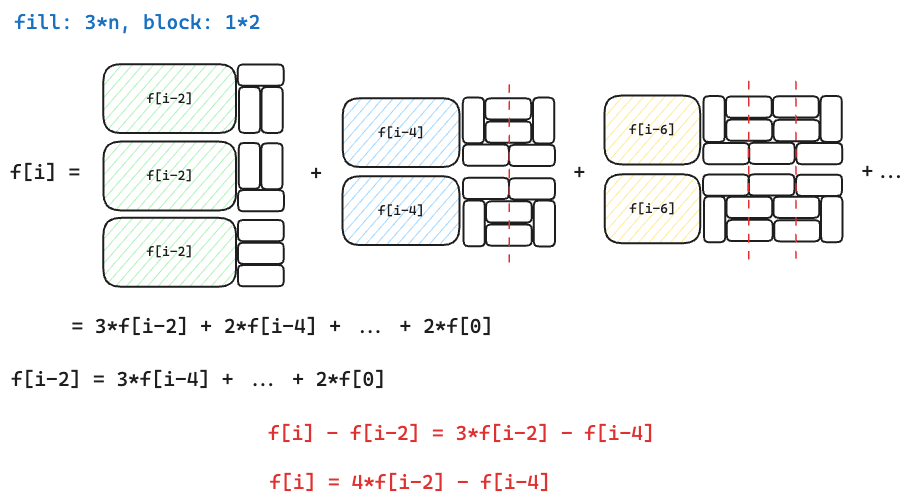
A 砖 $1 * 2$：n 为偶 $dp[i] = 4 * dp[i - 2] - dp[i - 4]$，n 为奇 $dp[i]=0$

POJ - 2663 Tri Tiling

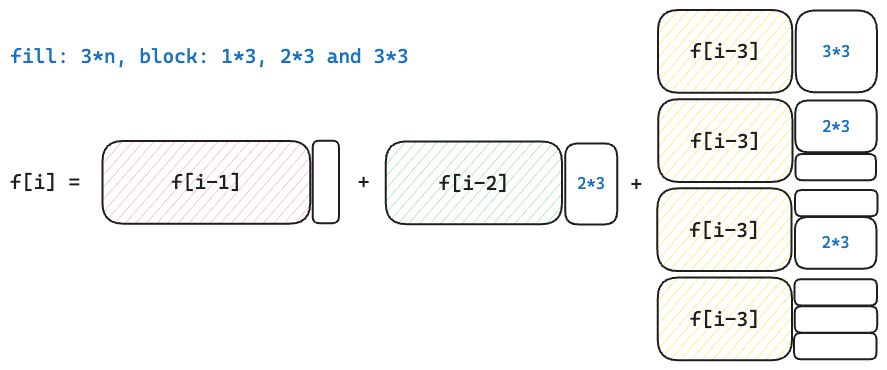
A 砖 $1 * 3$，B 砖 $2 * 3$，C 砖 $3 * 3$：$dp[i] = dp[i - 1] + dp[i - 2] + 4 * dp[i - 3]$

dp[1] = 1, dp[2] = 2, dp[3] = 7

扩展

不仅有计算指定墙面下有多少种铺法的题目，还有求铺满指定墙面消耗瓷砖最少的铺法，以及判断是否能铺满的题目。

$M * N$ 墙面方案数

铺瓷砖问题(状态压缩动态规划)：在一个 N 行 M 列的格子里，现有 1*2 大小的瓷砖，可以横着或者竖着铺。问一共有多少种方案，可以将整个 N*M 的空间都填满

最优性

1240. 铺瓷砖：墙面：n * m，瓷砖：正方形瓷砖，目标：最少需要用到多少块方形瓷砖？

可行性

题目：用 1 * 2 的砖铺 m * n 的地面，地面上有一些障碍物，求是否可以不用切割砖块铺满地面，并计算时间复杂度。

思路：DFS，DP，和 Leetcode 迷宫、寻宝、地下城等问题相似

参考

• 题解：铺瓷砖（动态规划）
• 题解：灵茶山艾府