【算法专题】二叉树的遍历

2022-01-09 2023-12-29 约 1900 字预计阅读 4 分钟

二叉树的前/中/后序遍历有多种实现方法，其中递归遍历最为简单，这里额外介绍栈迭代、颜色标记等方法。

前序遍历

递归遍历

时间复杂度: ${O(n)}$
空间复杂度: ${O(h)}$，$h$ 是树的高度

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


class Solution {
public:
    vector<int> order;
    vector<int> preorderTraversal(TreeNode* root) {
        dfs(root);
        return order;
    }
    void dfs(TreeNode* u) {
        if (u == nullptr) return;
        order.push_back(u->val);
        dfs(u->left);
        dfs(u->right);
    }
};

栈迭代

时间复杂度: ${O(n)}$
空间复杂度: ${O(h)}$，$h$ 是树的高度

实现（一）直接访问左子节点；存右子结点

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


class Solution {
public:
    vector<int> order;
    vector<int> preorderTraversal(TreeNode* root) {
        if (root == nullptr) return {};
        stack<TreeNode*> sk;
        TreeNode* t = root;
        while (t || sk.size()) {
            while (t) {
                order.push_back(t->val);
                sk.push(t->right);
                t = t->left;
            }
            t = sk.top(); sk.pop();
        }
        return order;
    }
};

实现（二）直接访问左子节点；存左子结点，转至右子节点

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


class Solution {
public:
    vector<int> order;
    vector<int> preorderTraversal(TreeNode* root) {
        if (root == nullptr) return {};
        stack<TreeNode*> sk;
        TreeNode* t = root;
        while (t || sk.size()) {
            while (t) {
                order.push_back(t->val);
                sk.push(t);
                t = t->left;
            }
            t = sk.top(); sk.pop();
            t = t->right;
        }
        return order;
    }
};

实现（三）存右子结点后再存左子节点

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


class Solution {
public:
    vector<int> order;
    vector<int> preorderTraversal(TreeNode* root) {
        if (root == nullptr) return {};
        stack<TreeNode*> stk;
        stk.push(root);
        while (stk.size()) {
            TreeNode* t = stk.top(); stk.pop();
            order.push_back(t->val);
            if (t->right) stk.push(t->right);
            if (t->left) stk.push(t->left);
        }
        return order;
    }
};

颜色标记法

使用颜色标记节点的状态，新节点为白色 0，已访问的节点为灰色 1。如果遇到的节点为白色，则将其标记为灰色，然后将其 右子节点、左子节点、自身 依次入栈。如果遇到的节点为灰色，则将节点的值输出。

时间复杂度: ${O(n)}$
空间复杂度: ${O(h)}$，$h$ 是树的高度

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


class Solution {
typedef pair<TreeNode*, int> PTI;
public:
    vector<int> order;
    vector<int> preorderTraversal(TreeNode* root) {
        stack<PTI> stk;
        stk.push({root, 0});
        while (stk.size()) {
           auto [t, color] = stk.top(); stk.pop();
           if (t == nullptr) continue;
           if (color == 0) {
               stk.push({t->right, 0});
               stk.push({t->left, 0});
               stk.push({t, 1});
           } else {
               order.push_back(t->val);
           }
        }
        return order;
    }
};

中序遍历

leetcode-94. 二叉树的中序遍历

递归

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


class Solution {
public:
    vector<int> order;
    vector<int> inorderTraversal(TreeNode* root) {
        dfs(root);
        return order;
    }
    void dfs(TreeNode* u) {
        if (u == nullptr) return;
        dfs(u->left);
        order.push_back(u->val);
        dfs(u->right);
    }
};

栈迭代

出栈访问：不断往左边走，当左边走不下去了，就打印节点，并转向右边，然后右边继续这个过程

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


class Solution {
public:
    vector<int> order;
    vector<int> inorderTraversal(TreeNode* root) {
        stack<TreeNode*> stk;
        TreeNode* t = root;
        while (t || stk.size()) {
            // 不断往左走，路过节点入栈
            while (t) {
                stk.push(t);
                t = t->left;
            }
            // 左边走到头，取出栈顶的当前节点并加入序列，转向右节点
            t = stk.top(); stk.pop();
            order.push_back(t->val);
            t = t->right;
        }
        return order;
    }
};

莫里斯遍历

不使用任何辅助空间，但改变了整个树的结构，强行把一棵二叉树改成一段链表结构

时间复杂度: ${O(n)}$
空间复杂度: ${O(1)}$

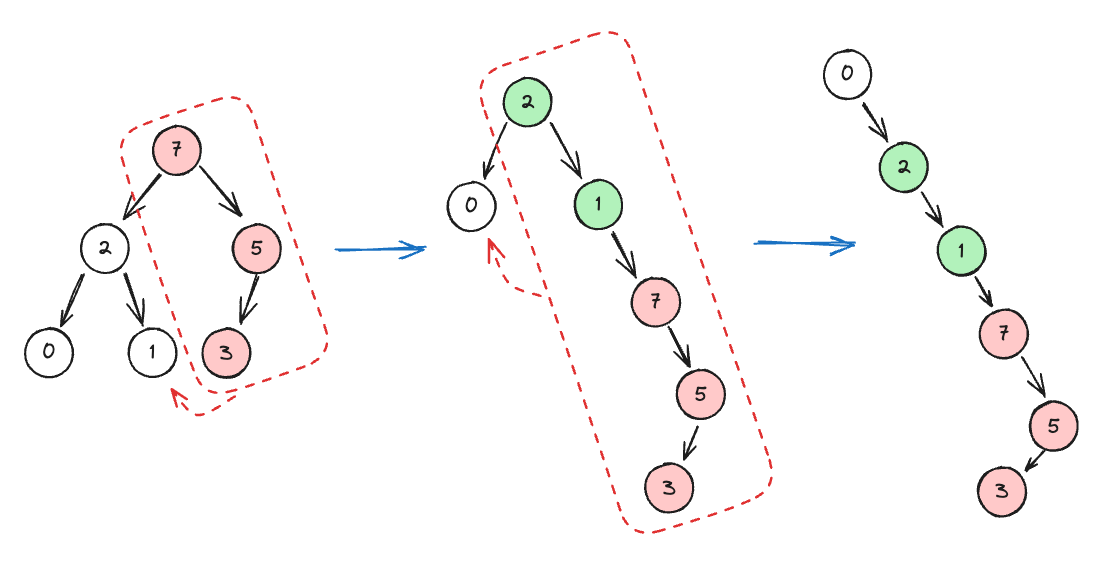
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> order;
        while (root) {
            if (root->left) {
                // 左子树非空，将（当前节点和其右子树）挂到（左节点的最右子树上）
                TreeNode* p = root->left;
                while (p->right) p = p->right;
                p->right = root;
                // 更新 root，root->left 置 nullptr
                TreeNode* t = root;
                root = root->left;
                t->left = nullptr;
            } else {
                // 左子树为空，打印这个节点，向右边遍历	
                order.push_back(root->val);
                root = root->right;
            }
        }
        return order;
    }
};

颜色标记法

使用颜色标记节点的状态，新节点为白色 0，已访问的节点为灰色 1。如果遇到的节点为白色，则将其标记为灰色，然后将其 右子节点、自身、左子节点 依次入栈。如果遇到的节点为灰色，则将节点的值输出。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


class Solution {
typedef pair<TreeNode*, int> PTI;
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> order;
        stack<PTI> stk;
        stk.push({root, 0});
        while (stk.size()) {
            auto [t, color] = stk.top(); stk.pop();
            if (t == nullptr) continue;
            if (color == 0) {
                stk.push({t->right, 0});
                stk.push({t, 1});
                stk.push({t->left, 0});
            } else {
                order.push_back(t->val);
            }
        }
        return order;
    }
};

后序遍历

leetcode-145. 二叉树的后序遍历

递归遍历

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


class Solution {
typedef pair<TreeNode*, int> PTI;
public:
    vector<int> order;
    vector<int> postorderTraversal(TreeNode* root) {
        dfs(root);
        return order;
    }
    void dfs(TreeNode* u) {
        if (u == nullptr) return;
        dfs(u->left);
        dfs(u->right);
        order.push_back(u->val);
    }
};

标记+栈迭代

初始为0，访问完左子树为1，访问完右子树出栈

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


class Solution {
public:
    vector<int> order;
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> sk;
        map<TreeNode*, bool> mp;
        TreeNode* t = root;
        while (t || sk.size()) {
            while (t) {
                sk.push(t);
                t = t->left;
            }
            while (sk.size() && mp[sk.top()]) {   // 从右子树返回
                order.push_back(sk.top()->val);
                sk.pop();
            }
            if (sk.size()) {
                t = sk.top(); mp[t] = true;       // 访问完左子树，访问右子树前
                t = t->right;
            }
        }
        return order;
    }
};

逆序+栈迭代

【左右根】→【根右左】，参照前序遍历的栈迭代写法，最后将序列翻转即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


class Solution {
public:
    vector<int> order;
    vector<int> postorderTraversal(TreeNode* root) {
        if (root == nullptr) return {};
        stack<TreeNode*> sk;
        TreeNode* t = root;
        while (t || sk.size()) {
            while (t) {
                order.push_back(t->val);
                sk.push(t->left);
                t = t->right;
            }
            t = sk.top(); sk.pop();
        }
        reverse(order.begin(), order.end());
        return order;
    }
};

颜色标记法

使用颜色标记节点的状态，新节点为白色 0，已访问的节点为灰色 1。如果遇到的节点为白色，则将其标记为灰色，然后将其 自身、右子节点、左子节点 依次入栈。如果遇到的节点为灰色，则将节点的值输出。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


class Solution {
typedef pair<TreeNode*, int> PTI;
public:
    vector<int> order;
    vector<int> postorderTraversal(TreeNode* root) {
        stack<PTI> stk;
        stk.push({root, 0});
        while (stk.size()) {
           auto [t, color] = stk.top(); stk.pop();
           if (t == nullptr) continue;
           if (color == 0) {
               stk.push({t, 1});
               stk.push({t->right, 0});
               stk.push({t->left, 0});
           } else {
               order.push_back(t->val);
           }
        }
        return order;
    }
};

总结

递归最为简单，直观易懂，代码实现方便，但效率不高；
栈迭代效率高但写法难度大，嵌套循环不易理解，不同的遍历顺序（前序、中序、后序）循环结构差异大；
颜色标记法是一种通用且简明的非递归二叉树遍历方法。

Reference

收录于合集・算法笔记 14

【算法笔记】7.动态规划【算法专题】铺瓷砖