【算法笔记】0.开篇

2021-01-31 2024-02-01 约 1500 字预计阅读 3 分钟

此文是算法笔记系列的开篇，介绍算法竞赛的赛制以及做题技巧，并整理算法相关资料，方便日后查阅。

赛制分类

赛制	是否罚时	分数计算方法	结果反馈
ACM	✅	全部测试点通过才得分	✅
IO	❌	按测试点给分	❌
IOI	❌	按测试点给分	✅

算法的时间复杂度「Time Complexity」是一个函数，它定性描述算法的运行时间。它是渐近的，即考察输入值大小趋近无穷时的情况，不是用来代表算法的实际执行时间，而是用于表示代码执行时间的增长变化趋势。

时间复杂度常用大 O 符号 $O(n)$ 表述，大 O 符号，又称渐进符号，是用于描述函数渐近上界的数学符号。

$O(n)$ 数学定义：假如存在正实数 M 和实数 x0，使得对于所有的 x ≥ x0，均有：$|f(x)| ≤ M |g(x)|$ 成立，我们就可以认为，$f(x)=O(g(x))$

$O(log_m^n)$ 通过对数的换底公式，可以得到具有不同底数、相等的时间复杂度，因此通常省略底数，将对数阶直接记为 $O(logn)$

当 $n>=4$ 时恒有 $n! >= 2^n$，所以阶乘阶比指数阶增长得更快！

渐进表示符号如下表「最差（渐进上界）$O$；最佳（渐进下界）$\Omega$；平均 $\Theta$，但常被 $O$ 替代」

实际中很少使用最佳时间复杂度，因为通常只有在很小概率下才能达到，可能会带来一定的误导性。而最差时间复杂度更为实用，因为它给出了一个效率安全值，让我们可以放心地使用算法。

平均时间复杂度可以体现算法在随机输入数据下的运行效率，但对于较为复杂的算法，计算平均时间复杂度往往比较困难，因为很难分析出在数据分布下的整体数学期望。在这种情况下，我们通常使用最差时间复杂度作为算法效率的评判标准。

空间复杂度「Space Complexity」是对一个算法在运行过程中临时占用内存空间大小的一个量度，反映的是随着数据量变大时的增长趋势。

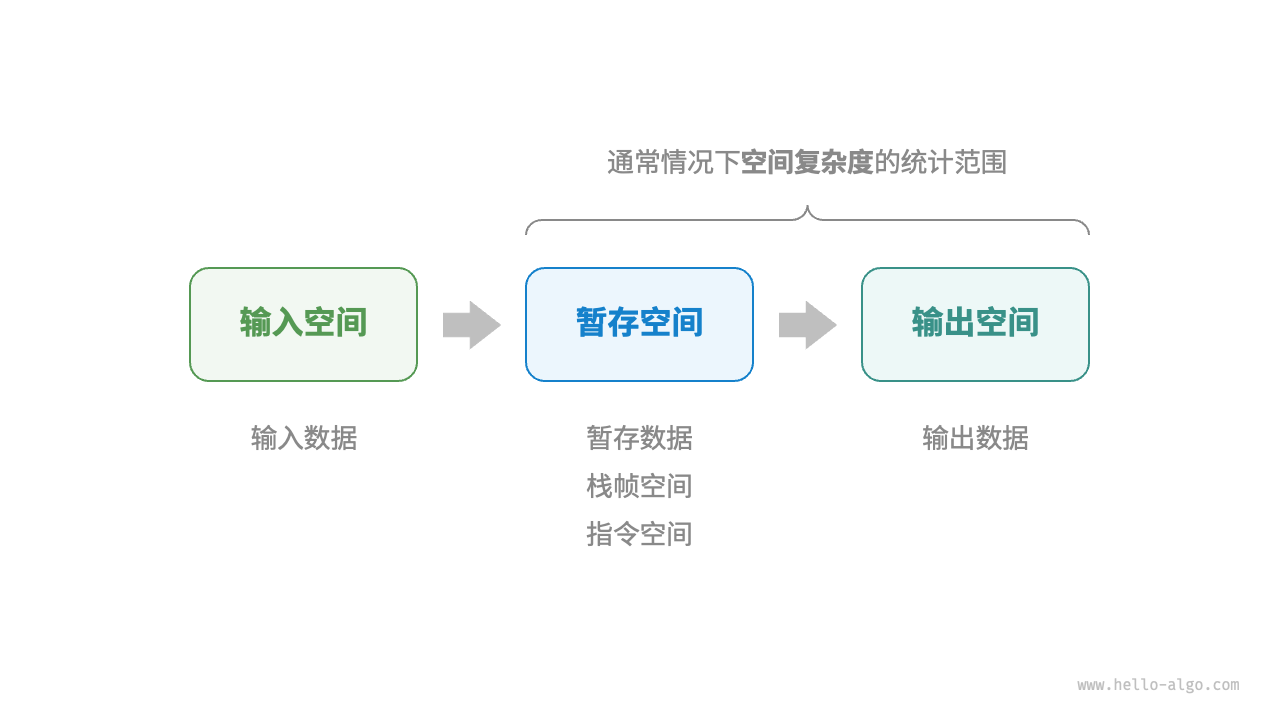
在分析一段程序的空间复杂度时，我们通常统计暂存数据、栈帧空间和输出数据三部分。

与时间复杂度不同的是，我们通常只关注最差空间复杂度。这是因为内存空间是一项硬性要求，我们必须确保在所有输入数据下都有足够的内存空间预留。

一般ACM或者笔试题的时间限制是1秒或2秒，在这种情况下，C++代码中的操作次数控制在 $10^7 \sim 10^8$ 为最佳。

根据题目给出的数据范围可反推算法复杂度以及算法内容，下面给出不同数据范围下的代码时间复杂度和算法该如何选择：

数据范围	代码的时间复杂度	算法选择
$n \le 30$	指数级别	DFS+剪枝，状态压缩DP
$n \le 100$	$O(n^3)$	Floyd，DP，高斯消元
$n \le 1000$	$O(n^2)$，$O(n^2logn)$	DP，二分，朴素版Dijkstra、朴素版Prim、Bellman-Ford
$n \le 10^4$	$O(n * \sqrt n)$	块状链表、分块、莫队
$n \le 10^5$	$O(nlogn)$	各种sort、线段树、树状数组、set/map、heap、拓扑排序、Dijkstra+heap、Prim+heap、Kruskal、SPFA、求凸包、求半平面交、二分、CDQ分治、整体二分、后缀数组、树链剖分、动态树
$n \le 10^6$	$O(n)$ 常数较小的 $O(nlogn)$	单调队列、hash、双指针扫描、BFS、并查集，KMP、AC自动机，常数较小的 $O(nlogn)$ 做法：sort、树状数组、heap、Dijkstra、SPFA
$n \le 10^{7/8}$	$O(n)$	双指针扫描、KMP、AC自动机、线性筛素数
$n \le 10^9$	$O(\sqrt n)$	判断质数
$n \le 10^{18}$	$O(logn)$	最大公约数，快速幂，数位DP
$n \le 10^{1000}$	$O((logn)^2)$	高精度加减乘除
$n \le 10^{100000}$	$O(logk \times loglogk)，k表示位数$	高精度加减、FFT/NTT