区间问题
区间选点
905. 区间选点:
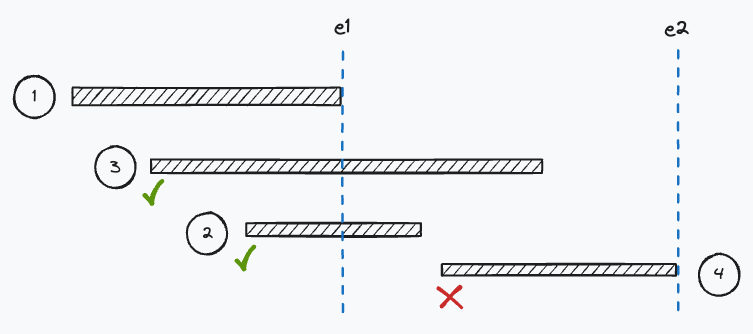
给定 N 个闭区间 $[a_i,b_i]$,请你选择尽量少的点,使得每个区间内至少包含一个选出的点(位于区间端点上的点也算作区间内),输出选择的点的最小数量。
-
将所有区间按照右端点从小到大进行排序
-
从前往后依次枚举每个区间,初始点 e 选为无穷小
-
如果当前区间已经包含该点,直接跳过
-
否则,选择当前区间的右端点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
#include <iostream>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e5+10;
PII range[N];
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
int l, r;
cin >> l >> r;
range[i] = {r, l}; // 以区间右端点,从小到大排序
}
sort(range, range + n);
int res = 0, e = -2e9; // e 初始为最小值
for (int i = 0; i < n; i++) {
int l = range[i].second, r = range[i].first;
if (l > e) {
e = r;
res++;
}
}
cout << res;
return 0;
}
|
最大不相交区间数量
908. 最大不相交区间数量:
给定 N 个闭区间 $[a_i,b_i]$,请你在数轴上选择若干区间,使得选中的区间之间互不相交(包括端点),输出可选取区间的最大数量。
此题与上节 区间选点 解法一致
区间分组
906. 区间分组:
给定 N 个闭区间 $[a_i,b_i]$,请你将这些区间分成若干组,使得每组内部的区间两两之间(包括端点)没有交集,并使得组数尽可能小。
-
将所有区间按照左端点从小到大进行排序
-
从前往后依次处理每个区间,判断是否能放到某个现有的组中($L[i] > 该组的 max(r)$)
-
如果不存在这样的组,新开一组放入
-
如果存在这样的组,放入其中,并更新当前组的 $max(r)$
使用小根堆得到各组 $max(r)$ 的最小值,直接比较最小值即可快速判断是否存在满足条件的组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e5+10;
PII range[N];
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
int l, r;
cin >> l >> r;
range[i] = {l, r}; // 以区间左端点,从小到大排序
}
sort(range, range + n);
// 小根堆,存每组中的最右端点
priority_queue<int, vector<int>, greater<int>> heap;
for (int i = 0; i < n; i++) {
int l = range[i].first, r = range[i].second;
if (heap.empty() || l <= heap.top()) {
// heap 为空 or 不能插入现有组
heap.push(r);
} else {
// 插入现有最右端点最小的组,更新
heap.pop();
heap.push(r);
}
}
cout << heap.size();
return 0;
}
|
把求区间厚度的问题类比成活动安排问题:有若干个活动,第 i 个活动开始时间和结束时间是 $[Si,fi]$,同一个教室安排的活动之间不能交叠,求要安排所有活动,少需要几个教室?题解
有时间冲突的活动不能安排在同一间教室,与该问题的限制条件相同,即最小需要的教室个数即为该题答案。
我们可以把所有开始时间和结束时间排序,遇到开始时间就把需要的教室加 1,遇到结束时间就把需要的教室减 1,在一系列需要的教室个数变化的过程中,峰值就是多同时进行的活动数,也是我们至少需要的教室数。
为了在排序不变的情况下区分开始、结束时间,对原区间的左右端点进行奇偶预处理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 1e5+10;
int time[N*2];
int main() {
int n;
cin >> n;
for (int i = 0, idx = 0; i < n; i++) {
int l, r;
cin >> l >> r;
time[idx++] = l * 2; // 奇数代表起始点(左端点)
time[idx++] = r * 2 + 1; // 偶数代表结束点(右端点)
}
sort(time, time + n*2);
int res = 0, cur = 0;
for (int i = 0; i < 2 * n; i++) {
if (time[i] % 2 == 0) cur++;
else cur--;
res = max(res, cur);
}
cout << res;
return 0;
}
|
区间合并
56. 合并区间:
请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间
-
将所有区间按照左端点从小到大进行排序
-
从前往后依次处理每个区间,判断是否能放到当前合并区间中($L[i]$ <= 当前合并区间的 $r$)
-
如果不符合,新开一组放入
-
如果符合,放入其中,并更新当前合并区间的 $r$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
int n = intervals.size();
vector<vector<int> > ans;
sort(intervals.begin(), intervals.end());
for (int i = 0; i < n; i++) {
int l = intervals[i][0], r = intervals[i][1];
if (ans.empty() || l > ans.back()[1]) {
// 添加一个新的区间
ans.push_back({l, r});
} else {
// 加入现有区间,更新需要取 max [[1,4],[2,3]]
ans.back()[1] = max(ans.back()[1], r);
}
}
return ans;
}
};
|
区间覆盖
907. 区间覆盖:
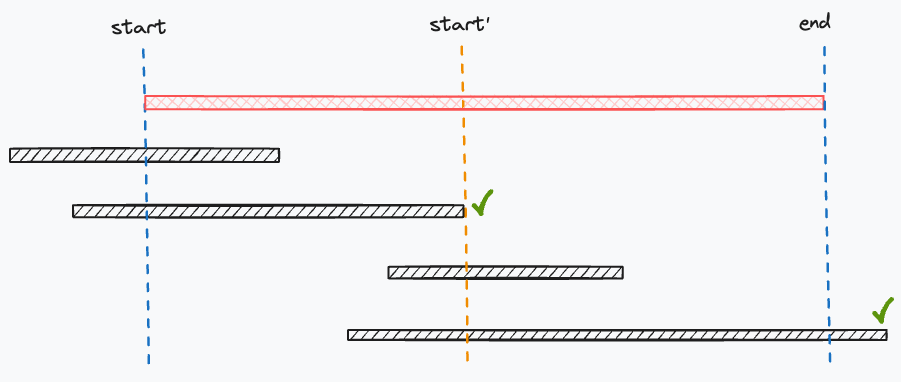
给定 N 个闭区间 $[a_i,b_i]$,以及一个线段区间 $[s,t]$,请你选择尽量少的区间,将指定线段区间完全覆盖。输出最少区间数,如果无法完全覆盖则输出 −1。
-
将所有区间按照左端点从小到大进行排序
-
从前往后依次处理每个区间,在所有能覆盖 start 的区间中选择右端点最大的,然后将 start 更新为该点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1e5+10;
pair<int, int> range[N];
int main() {
int n, st, ed;
cin >> st >> ed >> n;
for (int i = 0; i < n; i++ ) {
int l, r;
cin >> l >> r;
range[i] = {l, r}; // 以区间左端点,从小到大排序
}
sort(range, range + n);
int res = 0;
bool success = false;
for (int i = 0; i < n; i++) {
// 找到可以覆盖左端点 且 右端点最大的区间
int j = i, r = -2e9;
while (j < n && range[j].first <= st) {
r = max(r, range[j].second);
j++;
}
if (r < st) break; // 不存在连续区间可以覆盖
res++;
if (r >= ed) { // 目标区间覆盖完毕
success = true;
break;
}
st = r; // 更新原区间需要覆盖的开头
i = j - 1; // 查找下一个区间 (i++ 后 i=j 下一轮从 j 开始)
}
if (!success) res = -1;
cout << res << endl;
return 0;
}
|
Huffman 树
选出根结点的权值最小的两棵树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和,不断递归直到只剩下一个树,便得到了 Huffman 树。树上权值小的远离根,权值大的靠近根,树的带权路径长度最小。
Huffman 编码:对于 Huffman 树的每个叶子结点,从根到该结点的路径上,向左走则编码为 0,向右走则编码为 1;是无损压缩的变长编码。
148. 合并果子
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
#include <iostream>
#include <queue>
using namespace std;
int main() {
int n;
cin >> n;
// 小根堆
priority_queue<int, vector<int>, greater<int>> hp;
for (int i = 0; i < n; i++) {
int x;
cin >> x;
hp.push(x);
}
int res = 0;
while (hp.size() > 1) {
int a = hp.top(); hp.pop();
int b = hp.top(); hp.pop();
res += a + b;
hp.push(a + b);
}
cout << res;
return 0;
}
|
排序不等式
排队打水
对任务按时间降序排序 $T_1, T_2, \ldots T_n$,先完成耗时长的任务,则整体等待时间最少,为:
$T_1*(n-1) + T_2*(n-2) + … + T_{n-1}*1 + T_n * 0$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5+10;
int t[N];
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) cin >> t[i];
long long res = 0;
sort(t, t + n);
for (int i = 0; i < n; i++) {
res += t[i] * (n - i - 1);
}
cout << res;
return 0;
}
|
绝对值不等式
货仓选址:
在一条数轴上有 N 家商店,它们的坐标分别为 $A_1∼A_n$。现在需要在数轴上建立一家货仓,每天清晨,从货仓到每家商店都要运送一车商品。
求把货仓建在何处,可以使得货仓到每家商店的距离之和最小。
点的个数为 n,n 为奇数取中位数,n 为偶数取中间两数之间的任意数。可见 A[n / 2] 就是答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5+10;
int a[N];
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) cin >> a[i];
sort(a, a + n);
int res = 0;
for (int i = 0; i < n; i++) {
res += abs(a[i] - a[n / 2]); // n / 2 恰好满足奇偶情况,不用额外区分
}
cout << res;
return 0;
}
|
依据 $\sum_{i=0}^{n-1}(a_i-a_{n/2})=\sum_{i=0}^{n-1}(a_i-a_{i/2})$,下面的计算等价
1
2
3
|
for (int i = 0; i < n; i++) {
res += abs(a[i] - a[i / 2]);
}
|
1
2
3
4
5
6
7
|
// 快速求出中位数:将第 n/2 个元素放在正确的排序位置上,但不完全排序整个范围
// 以 a[n/2] 为界进行分区(左侧元素 < a[n/2],右侧 >),其他元素的相对顺序不能保证
nth_element(a, a + n / 2, a + n);
int res = 0;
for (int i = 0; i < n; i++) {
res += abs(a[i] - a[n / 2]);
}
|
可将一维扩展到二维,甚至 d 维度(模拟退火)
推公式
耍杂技的牛:
N 头奶牛垂直堆叠,每一头都有着自己的重量 $w_i$ 以及自己的强壮程度 $s_i$。
一头牛支撑不住的可能性取决于它头上所有牛的总重量(不包括它自己)减去它的身体强壮程度的值,现在称该数值为风险值,风险值越大,这只牛撑不住的可能性越高。
您的任务是确定奶牛的排序,使得所有奶牛的风险值中的最大值尽可能的小。
从上到下记牛的编号为 $1-n$,就是找出一种牛的排列方式,令 $max(w_{1}+···+w_{i-1}-s_{i})$ 最小,记这个值为 $val$。
为了求排序的方案,可以交换 $i$, $i+1$ 牛的位置,看看满足什么等价条件,就可以使得交换之后 $val$ 不比之前大。
注意到交换 $i, i+1$ 牛的位置不会影响其他牛的风险度,故只需考察这两头牛
交换前:
牛 $i$: $w_{1}+···+w_{i-1}-s_{i}$ $①$
牛 $i+1$: $w_{1}+···+w_{i-1}+w_{i}-s_{i+1}$ $②$
交换后:
牛 $i$: $w_{1}+···+w_{i-1}+w_{i+1}-s_{i}$ $③$
牛 $i+1$: $w_{1}+···+w_{i-1}-s_{i+1}$ $④$
$val$ 不比之前大,即 $max(①,②) \geqslant max(③,④)$,其等价条件为:
$$max(-s_{i},w_{i}-s_{i+1})\geqslant max(w_{i+1}-s_{i},-s_{i+1})$$
若 $-s_{i} > w_{i}-s_{i+1}$ , $max(-s_{i},w_{i}-s_{i+1})=-s_i$,但 $-s_{i} < w_{i+1}-s_{i}$ 矛盾,故有 $-s_{i} \leqslant w_{i}-s_{i+1}$
故上式等价于:
$$w_{i}-s_{i+1} \geqslant max(w_{i+1}-s_{i},-s_{i+1})$$
显然 $w_{i}-s_{i+1} > -s_{i+1}$
于是:
$$w_{i}-s_{i+1}\geqslant w_{i+1}-s_{i}$$
即:
$$w_{i}+s_{i}\geqslant w_{i+1}+s_{i+1}$$
这意味着当 $w_{i}+s_{i}\geqslant w_{i+1}+s_{i+1}$ 时,交换 $i$, $i+1$ 牛的位置 $val$ 不比之前大,
即从上到下满足:$w_{i}+s_{i}$ 值递增。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
#include <iostream>
#include <algorithm>
#include <climits> // INT_MIN
using namespace std;
typedef pair<int, int> PII;
const int N = 5e4+10;
PII cows[N];
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
int w, s;
cin >> w >> s;
cows[i] = {w + s, w};
}
// 从小到大
sort(cows, cows + n);
int sum = 0, res = INT_MIN;
for (int i = 0; i < n; i++) {
int w = cows[i].second, s = cows[i].first - w;
res = max(res, sum - s);
sum += w;
}
cout << res;
return 0;
}
|
类似题目国王游戏:
乘除法推公式 + 高精度运算

