飞行日记Alfly's blog
飞行日记Alfly's blog

【算法笔记】4.数学问题

Alfly Alfly 收录于 笔记 和 算法笔记
  约 8100 字 预计阅读 16 分钟 

质数

质数的判定

试除法 $O(sqrt(n))$

1
2
3
4
5
6
7
8

// 判定质数
bool is_prime(int x) {
    if (x < 2) return false;
    for (int i = 2; i <= x / i; i++) {
        if (x % i == 0) return false;
    }
    return true;
}

以下写法不推荐

1
2
3
4

// sqrt() 开销大
for(int i = 2; i <= (int)sqrt(1.0 * x); i++)
// i * i 可能溢出
for(int i = 2; i * i <= x; i++)

分解质因数

试除法 $O(log(n))$ ~ $O(sqrt(n))$，当 $n = 2^k $，时间复杂度 $O(log(n))$

n 中最多只含一个大于 $sqrt(n)$ 的质因数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

void divide(int x) {
    for (int i = 2; i <= x / i; i++) {
        if (x % i == 0) {
            int cnt = 0;
            while (x % i == 0){
                x /= i;
                cnt++;
            }
            printf("%d %d\n", i, cnt);
        }
    }
    // 最后一个 > sqrt(x) 的质因数
    if (x > 1) printf("%d %d\n", x, 1);
    puts("");
}

筛质数

质数定理：1~n 中有 $n/ln(n)$ 个质数

朴素筛法

将每个数的倍数筛去 $O(nlog(n))$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

const int N = 1000010;
int primes[N], cnt;
bool st[N];

// 朴素筛质数
void get_primes(int n) {
    // 从 2 开始逐个筛选
    for (int i = 2; i <= n; i++) {
        if (!st[i]) {
            primes[cnt++] = i;
        }
        // 将当前数的倍数筛去
        for (int j = i + i; j <= n; j += i) {
            st[j] = true;
        }
    }
}

埃式筛法

将质数的倍数筛去 $O(nloglog(n))$

判断当前数 $x$ 是不是质数，只看前 $1 - x$ 个数中的质数能否把 $x$ 筛去。 因为若前 $1 - x$ 个数中的合数 $a$ 能消去 $x$，此前的 $x$ 一定已经被筛去了，不用重复筛。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

// 埃式筛质数
void get_primes(int n) {
    for (int i = 2; i <= n; i++) {
        if (!st[i]) {
            primes[cnt++] = i;
            // 将当前质数的倍数筛去
            for (int j = i + i; j <= n; j += i) {
                st[j] = true;
            }
        }
    }
}

线性筛法（欧拉）

每个数只会被其最小质因子筛去，即每个数只被筛一次：$O(n)$

  • 每次筛去 $n$ 的是其最小质数 $p_j$ ($ n = p_j * i$)
    • $i \bmod p_j \neq 0$ 时，$p_j$ 是 $n$ 的最小质数
    • $i \bmod p_j = 0$ 时，$p_j$ 是 $n$ 的最小质数
  • 每个合数都有唯一的最小质因数，每个合数都会被筛去，且仅被筛去一次
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

// 线性筛质数
memset(st, 0, sizeof st);
st[0] = st[1] = true;
void get_primes(int n) {
    for (int i = 2; i <= n; i++) {
        if (!st[i]) {
            primes[cnt++] = i;
        }
        for (int j = 0; primes[j] <= n / i; j++) { // 不需要 j < cnt 
            st[primes[j] * i] = true;          
            if (i % primes[j] == 0) break;
        }
    }
}

为什么不需要 j < cnt？

  1. 若 i 为质数, $p_j$ = i 时 退出 (j == cnt -1)
  2. 若 i 为合数, $p_j$ = i 的最小质因数时 退出 (j < cnt -1)

视频讲解：Bilibili，Python 版本

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

st = [True] * 2 + [False] * (n - 1)
def euler_sieve():
	for i in range(2, n + 1):
		if not st[i]:
			primes.append(i)
		for pj in primes:
			if pj * i > n:
				break
			st[pj * i] = True
			if i % pj == 0:
				break

约数

求约数

试除法 $O(sqrt(n))$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

vector<int> get_divisor(int n) {
    vector<int> res;
    for (int i = 1; i <= n / i; i++) {
        if (n % i == 0) {
            res.push_back(i);
            if (i != n / i) res.push_back(n / i);
        }
    }
    sort(res.begin(), res.end());
    return res;
}

最大公约数

辗转相除法（欧几里得法）

$a \% b = a - (a / b) * b = a - c * b$

$gcd(a, b) = gcd(b, a - c * b) ⇒ gcd(a, b) = gcd(b, a \% b)$

1
2
3
4
5
6
7
8
9

int gcd(int a, int b) {
    if (b == 0) return a;
    else return gcd(b, a % b);
}

// 浓缩写法
int gcd(int a, int b) {
    return b == 0 ? a : gcd(b, a % b);
}

其他解法：

  • 分解因式法（公约数 = 共同的因数乘积）
  • 更相减损法 $gcd(a, b) = gcd(b,a - b)$

约数个数

约数个数最多 1500 左右

约数个数定理：考虑任意一个数做质因数分解 $N = {p_1}^{\alpha_1} * {p_2}^{\alpha_2} * \ldots * {p_k}^{\alpha_k}$，

约数 $d = {p_1}^{\beta_1} * {p_2}^{\beta_2} * \ldots * {p_k}^{\beta_k}$，其中 $0 <= \beta_i <= \alpha_i$ 有 $\alpha_i + 1$ 种取值可能，则

约数个数 $num = (\alpha_1 + 1) * (\alpha_2 + 1) * \ldots * (\alpha_k + 1)$

$O(sqrt(n))$ 算法：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;

typedef long long LL;
const int N = 110, mod = 1e9+7;

int main() {
    int n;
    cin >> n;
    unordered_map<int, int> primes;
    // 分解质因数
    while (n--) {
        int x;
        cin >> x;
        for (int i = 2; i <= x / i; i++) {
            while (x % i == 0) {
                x /= i;
                primes[i] ++; 
            }
        }
        // 保存最后一个质因数
        if(x > 1) primes[x] ++;
    }
    
    LL ans = 1;
    for(auto p: primes) {
        ans = ans * (p.second + 1) % mod;
    }
    cout << ans;

    return 0;
}

约数之和

约数和定理：对于 $N = {p_1}^{\alpha_1} * {p_2}^{\alpha_2} * \ldots * {p_k}^{\alpha_k}$ ，则

N 的约数之和就是 $({p_1}^0 + {p_1}^1 + \ldots + {p_1}^{\alpha_1}) * \ldots * ({p_k}^0 + {p_k}^1 + \ldots + {p_k}^{\alpha_k})$。

给定 n 个正整数，输出这些数的乘积的约数之和，答案对$10^9+7$取模。

$O(sqrt(n))$ 算法：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

int main() {
    int n;
    cin >> n;
    unordered_map<int, int> primes;
    while (n--) {
        int x;
        cin >> x;
        for (int i = 2; i <= x / i; i++) {
            while(x % i == 0) {
                x /= i;
                primes[i]++; 
            }
        }
        if(x > 1) primes[x]++;
    }
    
    LL ans = 1;
    for (auto prime: primes) {
        LL t = 1;
        int p = prime.first, a = prime.second;
        // p^0 + p^1 + ... + p^a
        while (a--) {
            t = (t * p + 1) % mod;
        }
        ans = ans * t % mod;
    }
    cout << ans;
    return 0;
}

约数之和-变式

倍数

wiki-倍数

倍数性质

  • 0 是除了本身外任何数的倍数
  • 整数 n 和任何整数的乘积均为 n 的倍数
  • a 和 b 都是 x 的倍数，a + b 和 a - b 也是 x 的倍数

倍数判别：在十进制下，可以用一些较简单的方式判断整数是否为一些特定整数的倍数

  • 2 的倍数：个位数是偶数（0,2,4,6,8）
  • 3 的倍数：数字和是 3 的倍数
  • 4 的倍数：最末二位数是 4 的倍数（00,04,08）
  • 5 的倍数：个位数是 5 的倍数（0,5）
  • 6 的倍数：数字和是 3 的倍数，个位数又是偶数
  • 8 的倍数：最末三位数是 8 的倍数
  • 9 的倍数：若数字和是 9 的倍数
  • 10 的倍数：个位数为0
  • 11 的倍数：奇数位数字和和偶数位数字和的差为 11 的倍数（包括 0）
  • 25 的倍数：最末二位数是 25 的倍数（00,25,50,75）
  • 50 的倍数：末两位数为（00,50）
  • 100 的倍数：末两位数为 00
  • 末三位数是 000，（如 12345000）那个数就能被 1000 整除。

欧拉函数

对正整数 $n$，欧拉函数 $\varphi (n)$ 是 $<=n$ 的正整数中与$n$互质的数的个数。

在算数基本定理中，对于 $N = {p_1}^{\alpha_1} * {p_2}^{\alpha_2} * \ldots * {p_k}^{\alpha_k}$ ，则

$\varphi (n) = N * \frac{p_1 - 1}{p_1} * \frac{p_2 - 1}{p_2} * \ldots * \frac{p_k - 1}{p_k}$

依据容斥原理：

$\varphi (n) = N * (1 - \frac{1}{p_1}) * (1 - \frac{1}{p_2}) * \ldots * (1 - \frac{1}{p_k})$

$= N - \frac{N}{p_1} - \frac{N}{p_2} - \ldots - \frac{N}{p_k} + \frac{N}{p_1p_2} + \frac{N}{p_1p_3} + \ldots - \frac{N}{p_1p_2p_3} - \ldots + \frac{N}{p_1p_2p_3p_4} \ldots$

求欧拉函数

公式法 $O(sqrt(n))$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

int phi(int x) {
    int res = x;
    for (int i = 2; i <= x / i; i++) {
        if (x % i == 0) {
            res = res / i * (i - 1);
            while (x % i == 0) {
                x /= i;
            }
        }
    }
    if (x > 1) res = res / x * (x - 1);
    return res;
}

求 1~n 的所有欧拉函数

筛法递推 $O(n)$

https://imgs.alfly.cn/get-eulers.png

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

typedef long long LL;

const int N = 1000010;
int primes[N], cnt;
int phi[N];
bool st[N];
int n;

LL get_eulers(int n) {
    phi[1] = 1;
    for (int i = 2; i <= n; i++) {
        if (!st[i]) {
            primes[cnt++] = i;
            phi[i] = i - 1;
        }
        for (int j = 0; primes[j] <= n / i; j++) {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) {
                phi[primes[j] * i] = phi[i] * primes[j];
                break;
            } else {
                // phi[primes[j] * i] = primes[j] * phi[i] / primes[j] * (primes[j] - 1);
                phi[primes[j] * i] = phi[i] * (primes[j] - 1);
            }
        } 
    }
    LL res = 0;
    for (int i = 1; i <= n; i++) res += phi[i];
    return res;
}

快速乘/快速幂

快速乘

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

typedef long long LL;
// a*b % p
LL qmul(LL a, LL b, LL p) {
    LL res = 0;
    while (b) {
        if (b & 1) res = (res + a) % p;
        a = (a + a) % p;
        b >>= 1;
    }
    return res;
}

快速幂

迭代写法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

typedef long long LL;
// a^k % p
int qmi(int a, int k, int p) {
    int res = 1;
    while (k) {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

递归写法

1
2
3
4
5
6
7
8
9

typedef long long LL;
// a^k % p
int qmi(int a, int k, int p) {
    if (k == 0) return 1;
    a %= p;
    int res = qmi(a, k >> 1, p);
    if (k & 1) return res * res % p * a % p;
    return res * res % p;
}

快速幂求逆元

当 p 为质数，有：

$$ a/b \equiv a*b^{-1} \mod p$$

$$ b*b^{-1} \equiv 1 \mod p $$

由费马小定理可得 b 关于 p 的逆元为 $b^{p-2}$

$$b^{p-1} \equiv 1 \mod p$$

$$b * b^{p-2} \equiv 1 \mod p$$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

typedef long long LL;

// a^k % p
int qmi(int a, int k, int p) {
    int res = 1;
    while(k) {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

int main() {
    int n;
    cin >> n;
    while (n--) {
        int a, p;
        cin >> a >> p;
        // 费马小定理求 a 关于 p 的逆元
        int t = qmi(a, p - 2, p);
        
        // a % p == 0 时不存在 a 的逆元
        // 注意不能用 t == 0 来判断 p = 2 时情况特殊
        if (a % p) cout << t << '\n';
        else cout << "impossible" << '\n';
    }
    return 0;
}

扩展欧几里得算法

扩展欧几里得公式

$$gcd(a,b)= gcd(b,a\%b) = d $$

$$(a, b,x,y)->ax+by = d $$

$$(b,a\%b,y,x)->by+(a\%b)*x = d $$

$$by+(a\%b)*x = ax + b(y-ab*b)$$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

int exgcd(int a, int b, int &x, int &y) {
    if (b == 0) {
        x = 1, y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);

    // 递归求的是新系数，需要更正
    y -= a / b * x;
    return d;
}

int main() {
    int n;
    cin >> n;
    while (n--) {
        int a, b, x, y;
        scanf("%d%d", &a, &b);
        
        exgcd(a, b, x, y);
        printf("%d %d\n", x, y);
    }
    
    return 0;
}

线性同余方程

$$ ax \equiv b \mod m $$

$$ ax+my=b $$

gcd(a, m) | b 时有解

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

typedef long long LL;

int exgcd(int a, int b, int &x, int &y) {
    if(b == 0) {
        x = 1, y = 0;
        return a;
    }

    int d = exgcd(b, a % b, y, x);

    // 递归求的是新系数，需要更正
    y -= a / b * x;
    return d;
}

int main() {
    int n;
    cin >> n;
    while (n--) {
        int a, b, m, x, y;
        scanf("%d%d%d", &a, &b, &m);

        int d = exgcd(a, m, x, y);
        
        if (b % d != 0) puts("impossible");
        else printf("%d\n", (LL)x * (b / d) % m);
    }

    return 0;
}

中国剩余定理

一元线性同余方程组有解的准则以及求解方法

注意求解过程中应先检查同余式组上是否存在矛盾，存在矛盾的同余式组无解。

https://imgs.alfly.cn/chinese-remainder.png

不断合并两个方程—利用扩展欧几里得求解

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

typedef long long LL;

LL exgcd(LL a, LL b, LL &x, LL &y) {
    if (b == 0) {
        x = 1, y = 0;
        return a;
    }
    LL d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}

int main() {
    int n;
    cin >> n;
    
    bool has_answer = true;
    LL a1, m1;
    cin >> a1 >> m1;
    
    for (int i = 0; i < n -1; i++) {
        LL a2, m2;
        cin >> a2 >> m2;
        
        LL k1, k2;
        LL d = exgcd(a1, a2, k1, k2);
        if ((m2 - m1) % d) {
            has_answer = false;
            break;
        }
        
        k1 *= (m2 - m1) / d;
        // k1' = k1 + k * (a2 / d) 取模(a2 / d)的最小正整数
        LL t = a2 / d;
        k1 = (k1 % t + t) % t;
        // m1 = a1 * k1 + m1;
        m1 = a1 * k1 + m1;
        // a1 = lcm(a1, a2) = [a1, a2]
        a1 = abs(a1 / d * a2);
    }
    
    if (!has_answer) puts("-1");
    else cout << (m1 % a1 + a1) % a1;             // x mod a = m -> x = m
    
    return 0;
}

高斯消元

解线性方程组 $O(n^3)$

初等行列变换 → 行阶梯形矩阵

  1. 有唯一解：$R(A) = R(A,b) = n$
  2. 有无穷多解：$R(A) = R(A,b) < n$
  3. 无解：$R(A) < R(A,b)$

算法步骤：枚举每一列 C

  1. 选择绝对值最大的数所在的行 r
  2. 将该行换至最上（未固定的部分）
  3. 将该行第一个数变成 1
  4. 将该行下面的所有行的第 c 列变成 0，固定该行

高斯消元解线性方程组

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

const int N = 110;
const double eps = 1e-8;
double a[N][N];
int n;

// 高斯消元，答案存于a[i][n]中，0 <= i < n
int gauss() {
    int c, r;
    for (c = 0, r = 0; c < n; c++) {
        // 找绝对值最大的行
        int t = r;
        for (int i = r; i < n; i++)
            if (fabs(a[i][c]) > fabs(a[t][c]))
                t = i;
        
        // 最大值为 0 则进入下一列
        if (fabs(a[t][c]) < eps) continue;
        
        // 行换至顶端 且首位变成 1
        for (int i = c; i <= n; i++) swap(a[r][i], a[t][i]);
        for (int i = n; i >= c; i--) a[r][i] /= a[r][c];
        
        // 当前行下面的所有列消为 0
        for (int i = r + 1; i < n; i++)
            if (fabs(a[i][c]) > eps)
                for (int j = n; j >= c; j--)
                    a[i][j] -= a[r][j] * a[i][c];
        r ++;        
    }
    
    if (r < n) {
        for (int i = r; i < n; i++)
            if (fabs(a[i][n]) > eps)
                return 2;  // 无解
        return 1;  // 无穷组解
    }
    
    // 有唯一解，开始求解
    for (int i = n - 1; i >= 0; i--)
        for (int j = i + 1; j < n; j++)
            a[i][n] -= a[i][j] * a[j][n];
    return 0;
}

解异或线性方程组

https://imgs.alfly.cn/gauss.png

高斯消元解异或线性方程组

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

// 高斯消元，答案存于a[i][n]中，0 <= i < n
int gauss() {
    int c, r;
    for (c = 0, r = 0; c < n; c++) {
        // 找最大的行
        int t = r;
        for (int i = r; i < n; i++)
            if (a[i][c]) {
                t = i;
                break;
            }
        
        // 最大值为 0 则进入下一列
        if (!a[t][c]) continue;
        
        // 行换至顶端
        for (int i = c; i <= n; i++) swap(a[r][i], a[t][i]);
        
        // 当前行下面的所有列消为 0
        for (int i = r + 1; i < n; i++)
            if (a[i][c])
                for (int j = c; j <= n; j++)
                    a[i][j] ^= a[r][j];
        
        r ++;        
    }
    
    if (r < n) {
        for (int i = r; i < n; i++)
            if (a[i][n])
                return 2;  // 无解
        return 1;  // 无穷组解
    }
    
    // 有唯一解，开始求解
    for (int i = n - 1; i >= 0; i--)
        for (int j = i + 1; j < n; j++)
            a[i][n] ^= a[i][j] & a[j][n];
    return 0;  
}

求组合数

求 $C_a^b$，根据不同的数据量选择不同的算法

公式法

$$C_a^b = \frac{a!}{b! * (a - b)!} = \frac{a * (a-1) * \ldots * (a - b + 1)}{b!}$$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

int C(int a, int b) {
    int res = 1;
    int j = 1;
    for (int i = 0; i < b; i++) {
        res *= (a - i);
        while (j <= b && res % j == 0) {
            res /= j;
            j++;
        }
    }
    return res;
}

递推法

递推预处理得到所有 $C_a^b(C[a][b])$，时间复杂度 $O(n^2)$

$$C_a^b=C_{a-1}^b+C_{a-1}^{b-1}$$

$$c[i][j] = (c[i - 1][j] + c[i - 1][j - 1])$$

885. 求组合数 数据范围：$1≤n≤10000$，$1≤b≤a≤2000$

1
2
3
4
5
6
7
8
9

const int N = 2010, mod = 1e9 +7;
int c[N][N];

void init() {
    for (int i = 0; i < N; i++)
        for (int j = 0; j <= i; j++)
            if (j == 0) c[i][j] = 1;
            else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
}

递推预处理阶乘，时间复杂度 $O(nlogn)$

$$c[a][b] = \frac{a!}{b! * (a - b)!}$$

886. 求组合数 II 数据范围：$1≤n≤10000$，$1≤b≤a≤10^5$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

typedef long long LL;
const int N = 100010, mod = 1e9 + 7;

int fact[N], infact[N]; 

int qmi(int a, int k, int p) {
    int res = 1;
    while (k) {
        if(k & 1) res = (LL)res * a % p ;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

void init() {
    fact[0] = infact[0] = 1; 
    for (int i = 1; i < N; i ++) {
        fact[i] = (LL)fact[i -1] * i % mod;
        infact[i] = qmi(fact[i], mod - 2, mod);
    }
}

int a, b;
cin >> a >> b;
cout << (LL)fact[a] * infact[b] % mod * infact[a - b] % mod << '\n';

卢卡斯定理

时间复杂度 $O(log(n)*p*log(p))$

  • 当 a, b 特别大

$$C_a^b \equiv C_{a \mod p}^{b \mod p} * C_{a / p}^{b / p} \mod p$$

  • 当 a < p && b < p

$$C_a^b = \frac{a * (a-1) * \ldots * (a - b + 1)}{b!}$$

887. 求组合数 III 数据范围：$1≤n≤20$，$1≤b≤a≤10^{18}$，$1≤p≤10^5$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

typedef long long LL;
int p;

int qmi(int a, int k) {
    int res = 1;
    while(k) {
        if(k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

int C(int a, int b) {
    int res = 1;
    for (int i = 1, j = a; i <= b; i ++, j--) {
        res = (LL)res * j % p;
        res = (LL)res * qmi(i, p - 2) % p;
    }
    return res;
}

int lucas(LL a, LL b) {
    if (a < p && b < p) return C(a, b);
    else return (LL)C(a % p, b % p) * lucas(a / p, b / p) % p;
}

精确高精度计算

  1. 分解质因数
    1. 筛素数
    2. 求每个质数的数量
  2. 高精度乘法

888. 求组合数 IV 数据范围：$1≤b≤a≤5000$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

const int N = 5010;
int primes[N], cnt;
bool st[N];
int sum[N];

// 线性筛质数
void get_primes(int n) {
    for (int i = 2; i <= n; i++) {
        if (!st[i]) primes[cnt++] = i;
        for (int j = 0; primes[j] <= n / i; j++) {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

// n 含质因数 p 的个数
int get(int n, int p) {
    int res = 0;
    while(n) {
        res += n / p;
        n /= p;
    }
    return res;
}

// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b) {
    vector<int> res;
    int t = 0;
    for(int i = 0; i < A.size(); i ++) {
        t += A[i] * b;
        res.push_back(t % 10);
        t /= 10;
    }
    while(t) {
        res.push_back(t % 10);
        t /= 10;    
    }
    return res;
}

int main() {
    int a, b; 
    cin >> a >> b;
    
    get_primes(a);
    
    for (int i = 0; i < cnt; i++) {
        int p = primes[i];
        sum[i] = get(a, p) - get(b, p) - get(a - b, p);
    }
    
    vector<int> res;
    res.push_back(1);
    
    for (int i = 0; i < cnt; i++)
        for (int j = 0; j < sum[i]; j++)
            res = mul(res, primes[i]);
            
    for (int i = res.size() - 1; i >= 0; i--)
        printf("%d", res[i]);
    puts("");
    
    return 0;
}

卡特兰数

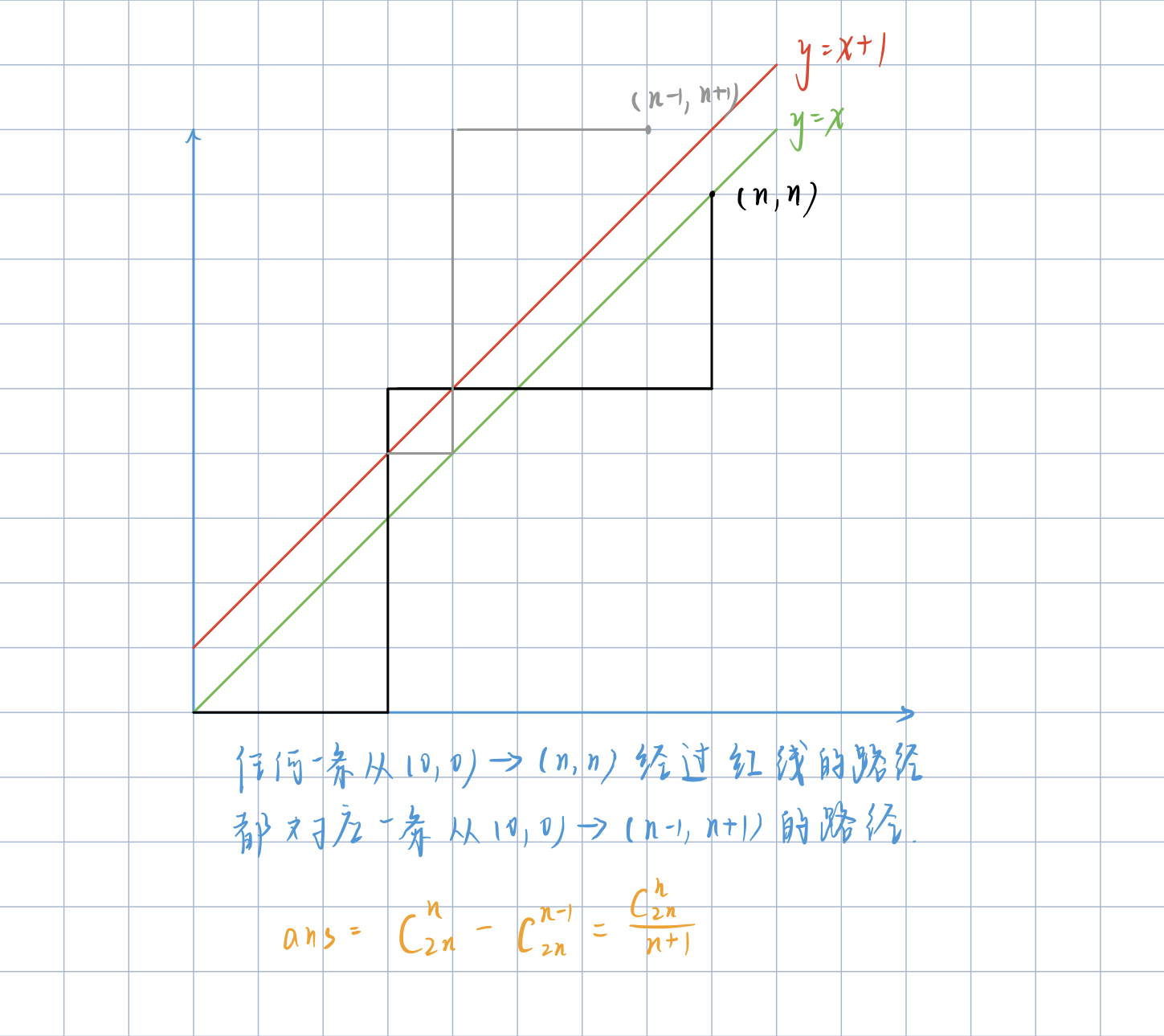
$$ {2n \choose n} - {2n \choose n -1} = {\frac{1}{n+1 }}{2n \choose n} $$

满足条件的01序列： 给定 n 个 0 和 n 个 1，它们将按照某种顺序排成长度为 2n 的序列，求所有序列中能满足任意前缀序列中 0 的个数都不少于 1 的个数的序列有多少个

https://imgs.alfly.cn/catalan.png

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

#include <iostream>
using namespace std;

typedef long long LL;
const int mod = 1e9+7;

int qmi(int a, int k, int p) {
    int res = 1;
    while (k) {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

int main() {
    int n;
    cin >> n;
    int a = 2 * n, b = n;
    
    int res = 1;
    for (int i = 1, j = a; i <= b; i++, j--) {
        res = (LL)res * j % mod;                    // * j
        res = (LL)res * qmi(i, mod - 2 ,mod) % mod; // /i
    }
    res = (LL)res * qmi(n + 1, mod - 2 ,mod) % mod; // /(n+1)
    cout << res;
    
    return 0;
}

容斥原理

$$\bigcup_{i=1}^{m} S_i = S_1 + S_2 + \ldots + S_m - (S_1 \bigcap S_2 + S_1 \bigcap S_3 +\ldots + S_{m-1} \bigcap S_m)$$

$$+ (S_1 \bigcap S_2 \bigcap S_3 +\ldots + S_{m-2} \bigcap S_{m-1} \bigcap S_m) + \ldots + (-1)^{m - 1} (\bigcap_{i=1}^{m}S)$$

能被整除的数： 给定一个整数 n 和 m 个不同的质数 $p_1,p_2,…,p_m$，请你求出 $1∼n$ 中能被 $p_1,p_2,…,p_m$ 中的至少一个数整除的整数有多少个。

使用位运算来处理集合

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

typedef long long LL;

const int N = 20;
int p[N];   // 质数

int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < m; i++) cin >> p[i];
    
    int res = 0;
    // 枚举质数集合状态
    for (int i = 1; i < 1 << m; i++) {
        int t = 1;      // 当前质数集合对应的乘积
        int cnt = 0;    // 集合数量
        for (int j = 0; j < m; j++) {
            if (i >> j & 1) {
                // 超过 n 则不可能有整除的数 (n/t = 0)
                if ((LL)t * p[j] > n) {
                    t = -1;
                    break;
                }
                cnt++;  // 记录集合数量
                t *= p[j];
            }  
        }
        if (t == -1) continue;
        // 容斥原理
        if (cnt % 2) res += n / t;  // 奇数个集合+，偶数个集合－
        else res -= n / t;
    }
    cout << res;
    
    return 0;
}

博弈论

  • K-Nim

Nim 游戏

若一个游戏满足以下三点，则称该游戏为一个公平组合游戏，Nim 游戏就属于公平组合游戏。

  • 由两名玩家交替行动
  • 在游戏进行的任意时刻，可以执行的合法行动与轮到哪位玩家无关
  • 不能行动的玩家判负

Nim 游戏-拿石子： 给定 $n$ 堆石子，两位玩家轮流操作，每次操作可以从任意一堆石子中拿走任意数量的石子（可以拿完，但不能不拿），最后无法进行操作的人视为失败。如果两人都采用最优策略，先手是否必胜。参考题解

例如：有两堆石子，第一堆有 2 个，第二堆有 3 个，先手必胜。

操作步骤：

  1. 先手从第二堆拿走1个，此时第一堆和第二堆数目相同
  2. 无论后手怎么拿，先手都在另外一堆石子中取走相同数量的石子即可。

先手必胜结论：假设 $n$ 堆石子，石子数目分别是 $a_1,a_2, \ldots ,a_n$，则有 $a_1 \oplus a_2 \oplus \ldots \oplus a_n \neq 0$ 先手必胜，$a_1 \oplus a_2 \oplus \ldots \oplus a_n = 0$ 先手必败

情况分析：

当 $a_1 \oplus a_2 \oplus \ldots \oplus a_n \neq 0$ 时，则一定存在 $a_i’$，将 $a_i→a_i’$ 后 $a_1 \oplus a_2 \oplus \ldots a_i’ \ldots \oplus a_n = 0$

证明：

当 $a_1 \oplus a_2 \oplus \ldots \oplus a_n = x (x ≠ 0)$，$a_1 至 a_n$ 中至少存在一个 $a_i$，其第 k 位为 1（x 最高位 1 是在第 k 位）。

则 $a_i \oplus x < a_i$ 满足拿走石子的条件，令 $a_i’ = a_i \oplus x$，有 $a_1 \oplus a_2 \oplus \ldots a_i’ \ldots \oplus a_n = 0$

当 $a_1 \oplus a_2 \oplus \ldots \oplus a_n = 0$ 时，则将 $a_i→a_i’$ 后，一定是 $a_1 \oplus a_2 \oplus \ldots a_i’ \ldots \oplus a_n \neq 0$

反证：

若 $a_1 \oplus a_2 \oplus \ldots a_i’ \ldots \oplus a_n = 0$，则 $a_i \oplus a_i’ = 0 → a_i = a_i’$，与 $a_i’ < a_i$ 矛盾。

操作到最后时，每堆石子数都是 $0$，$0 \oplus 0 \oplus \ldots \oplus 0 = 0$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

#include <iostream>
using namespace std;

int main() {
    int n;
    cin >> n;
    int res = 0;
    while (n--) {
        int k;
        cin >> k;
        res ^= k;
    }
    if (res) puts("Yes");
    else puts("No");
    return 0;
}

台阶-Nim游戏

Nim 游戏-台阶： 有一个 $n$ 级台阶的楼梯，每级台阶上都有若干个石子，其中第 $i$ 级台阶上有 $a_i$ 个石子$(i≥1)$。 两位玩家轮流操作，每次操作可以从任意一级台阶上拿若干个石子放到下一级台阶中（不能不拿）。 已经拿到地面上的石子不能再拿，最后无法进行操作的人视为失败。问如果两人都采用最优策略，先手是否必胜。

先手必胜结论：$a_1 \oplus a_3 \oplus \ldots \oplus a_n = 0$ 先手必败，$a_1 \oplus a_3 \oplus \ldots \oplus a_n \neq 0$ 先手必胜。

不顾偶数台阶，只考虑奇数台阶

  1. 对手从偶数台阶拿，自己从下一层拿相同数量
  2. 对手从奇数台阶拿，自己从奇数层拿使得奇数层异或为 0
  3. 自己永远不会到终点，即 $a_1, a_2, \ldots ,a_n = 0$
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

#include <iostream>
using namespace std;

int main() {
    int n;
    cin >> n;
    int res = 0;
    for (int i = 1; i <= n; i++) {
        int k;
        cin >> k;
        if (i % 2) res ^= k;
    }
    if (res) puts("Yes");
    else puts("No");
    return 0;
}

集合-Nim游戏

有向图游戏：给定一个有向无环图，图中有一个唯一的起点，起点上放一枚棋子。两名玩家交替沿有向边移动棋子，每次移动一步，无法移动者判负。把公平组合游戏中每个局面看成一个节点，有向边代表一个合法行动到达下一局面，便可转化为有向图游戏。

定义 $mex(A)$：不在集合 A 里的最小自然数。如：$mex(\{1, 2\}) = 0, mex(\{0, 1, 2\}) = 3$

当一个点的 $mex$ 值为 $0$，它一定只能到达 $mex$ 值不为 $0$ 的点

当一个点的 $mex$ 值不为 $0$，它一定可以到达 $mex$ 值为 $0$ 的点

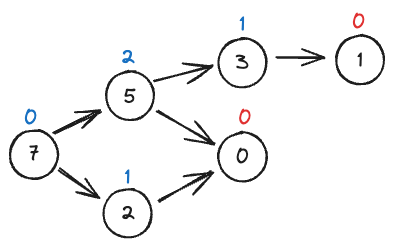
定义 $SG (x)$：若 $x$ 有出边 $(x,y_1),(x,y_2), \ldots ,(x,y_k)$，那么 $SG (x) = mex( \{ SG (y_1),SG (y_2), \ldots ,SG (y_k) \})$

当 $x$ 为终点，$SG(x) = 0$，计算有向图各个点的 $SG$ 值时从终点推导至起点

先手必胜结论：

  • 单个图 $G$，起点为 $s$

    $SG(s) = 0$ 先手必败

    $SG(s) \neq 0$ 先手必胜

  • 多图（$n$ 个游戏同时进行）

    $SG(s_1) \oplus SG(s_2) \oplus \ldots \oplus SG(s_n) = 0$ 先手必败

    $SG(s_1) \oplus SG(s_2) \oplus \ldots \oplus SG(s_n) \neq 0$ 先手必胜

Nim 游戏-集合： 给定 $n$ 堆石子以及一个由 $k$ 个不同正整数构成的数字集合 $S$。 现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合 $S$，最后无法进行操作的人视为失败。 如果两人都采用最优策略，先手是否必胜。

对于有石子数为 7 的石堆，$S = \{2, 5\}$ 时，有向图和 $SG(x)$ 计算如下：

https://imgs.alfly.cn/sg.png

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

#include <iostream>
#include <cstring>
#include <unordered_set>
using namespace std;

const int N = 110, M = 1e4+10;
int s[N];
int f[M];   // 存储 sg[] 用于记忆化搜索优化
int n, k;

// sg(x) = mex({sg(y1), sg(y2), ...})
int sg(int x) {
    if (f[x] != -1) return f[x];
    
    unordered_set<int> S;
    // 遍历集合 s 的所有操作,得到所有可达状态的 sg
    for (int i = 0; i < n; i++) {
        int sum = s[i];
        if (x >= sum) S.insert(sg(x - sum));
    }
    // mex(S): 遍历所有可达状态，找最小不可达
    for (int i = 0; ; i++) {
        if (S.count(i) == 0) {
            return f[x] = i;
        }
    }
}

int main() {
    cin >> n;
    for (int i = 0; i < n; i++) cin >> s[i];
    cin >> k;
    
    memset(f, -1, sizeof f);
    int res = 0;
    for (int i = 0; i < k; i++) {
        int x;
        cin >> x;
        res ^= sg(x);
    }
    if (res) cout << "Yes";
    else cout << "No";
    
    return 0;
}

拆分 - 局面增加

Nim 游戏-拆分： 给定 $n$ 堆石子，两位玩家轮流操作，每次操作可以取走其中的一堆石子，然后放入两堆规模更小的石子（新堆规模可以为 0，且两个新堆的石子总数可以大于取走的那堆石子数），最后无法进行操作的人视为失败。 问如果两人都采用最优策略，先手是否必胜。

相比于 集合-Nim，这里的每一堆可以变成小于原来那堆的任意大小的两堆。

一个局面拆分成了两个局面，由SG 函数理论，多个独立局面的 SG 值，等于这些局面 SG 值的异或和

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

#include <iostream>
#include <cstring>
#include <unordered_set>
using namespace std;

const int N = 110;
int f[N];   // 存储 sg[] 用于记忆化搜索优化

// sg(x) = mex({sg(y1), sg(y2), ...})
int sg(int x) {
    if (f[x] != -1) return f[x];
    
    unordered_set<int> S;
    // 分成两堆(i, j), 0 <= j <= i < x
    for (int i = 0; i < x; i++) {
        for (int j = 0; j <= i; j++) {
            S.insert(sg(i) ^ sg(j));
        }
    }
    // mex(S): 遍历所有可达状态，找最小不可达
    for (int i = 0; ; i++) {
        if (S.count(i) == 0) {
            return f[x] = i;
        }
    }
}

int main() {
    int n;
    cin >> n;
    
    memset(f, -1, sizeof f);
    int res = 0;
    for (int i = 0; i < n; i++) {
        int x;
        cin >> x;
        res ^= sg(x);
    }
    if (res) cout << "Yes";
    else cout << "No";
    
    return 0;
}
收录于 合集・算法笔记 14
更新于 2024-08-25 
CC BY-NC 4.0
阅读原始文档
算法数学
返回 | 主页
0%