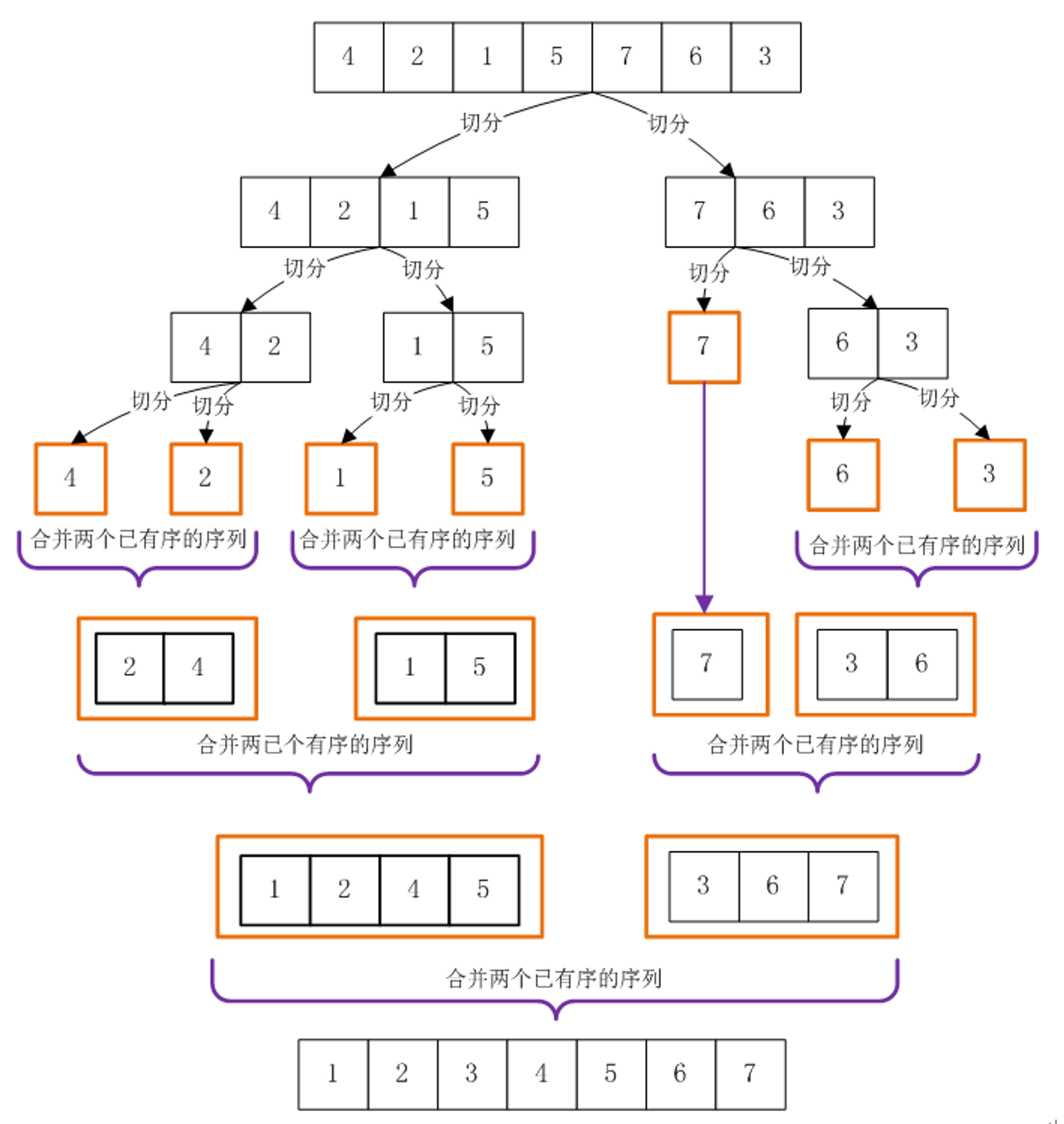
快速排序使用分治策略,把原始序列分为较小和较大的2个子序列,对这两个子序列递归排序,原理可见博客 。
例题-785. 快速排序 | 变式-786. 第k个数
x 可以取 左端点,中点,右端点,当取前三者中位数 时可有效防止退化到 $N^2$(当然也可以随机取点)
快速排序的实现可以按照划分方法分类,一下是常见的三类:
依次把序列中 $<x$ 的数放前面,$>x$ 的数放后面,每次划分后 x 是最终 位置,即 x 的左边一定全部比 x 小(右边同理)。
划分使用 $>=$, $<=$ 比较,当所有数相同时会 TLE
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void quick_sort ( int a [], int l , int r ) {
if ( l >= r ) return ;
swap ( a [( l + r ) >> 1 ], a [ l ]); // 把要取的点放在左端点
int x = a [ l ]; // 取左端点
int i = l , j = r ;
while ( i < j ) {
while ( i < j && a [ j ] >= x ) j -- ; // 先遍历 j 找 < x 的数
a [ i ] = a [ j ];
while ( i < j && a [ i ] <= x ) i ++ ;
a [ j ] = a [ i ];
}
a [ i ] = x ;
quick_sort ( a , l , i - 1 );
quick_sort ( a , i + 1 , r );
}
Lomuto partition 把比 $<x$ 的数统一放在最前面,每次划分后 x 是最终 位置,即 x 的左边一定全部比 x 小(右边同理)。
划分使用 $<=$ 比较,当所有数相同时会 TLE
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void quick_sort ( int a [], int l , int r ) {
if ( l >= r ) return ;
swap ( a [( l + r ) / 2 ], a [ r ]); // 把要取的点放在右端点
int x = a [ r ];
int i = l - 1 , j = l ;
while ( j <= r ) {
if ( a [ j ] <= x ) {
i ++ ;
swap ( a [ i ], a [ j ]);
}
j ++ ;
}
quick_sort ( a , l , i - 1 );
quick_sort ( a , i + 1 , r );
}
Hoare partition 进行分区时 $a[j]$ 并不是前 $k$ 个数的最大值,每次划分后 $x$ 不一定是最终位置,即 $x$ 的左边不一定全部比 $x$ 小(右边同理),但左区间一定小于右区间 。
划分使用 $>, <$(不含等号 )进行比较;
直接交换比较的顺序(先 $>$ 后 $<$)不能实现逆序,需要同时更改分区位置
注意代码不同取法的边界问题,下面 $i, j$ 不能混淆(每次划分 $i, j$ 不一定相等),可用特例 $[1, 2]$ 和 $[2, 1]$ 判断是否出现死循环来检查代码边界:
$[1, 2]$ 用于判断中间点的取值
配合 $[2, 1]$ 判断分区点是 i 还是 j
$[l, j], [j + 1, r]$:j 是最后一个小于或等于(=)基准的元素的位置,选择 j 作为分区点(左区间 ),可以确保左子数组的所有元素都小于或等于基准,而右子数组的所有元素都大于或等于基准
1
2
3
4
5
6
7
8
9
10
11
12
13
14
void quick_sort ( int a [], int l , int r ) {
if ( l >= r ) return ;
int x = a [( l + r ) / 2 ]; // 可取左端点,或下取整的中点
int i = l - 1 , j = r + 1 ;
while ( i < j ) {
do i ++ ; while ( a [ i ] < x );
do j -- ; while ( a [ j ] > x );
if ( i < j ) swap ( a [ i ], a [ j ]);
}
quick_sort ( a , l , j ); // [l, j], [j + 1, r]
quick_sort ( a , j + 1 , r );
}
$[l, i - 1], [i, r]$:i 是第一个大于或等于(=)基准的元素的位置,选择 i 作为分区点(右区间 )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
void quick_sort ( int a [], int l , int r ) {
if ( l >= r ) return ;
int x = a [( l + r + 1 ) / 2 ]; // 可取右端点,或上取整的中点
int i = l - 1 , j = r + 1 ;
while ( i < j ) {
do i ++ ; while ( a [ i ] < x );
do j -- ; while ( a [ j ] > x );
if ( i < j ) swap ( a [ i ], a [ j ]);
}
quick_sort ( a , l , i - 1 ); // [l, i - 1], [i, r]
quick_sort ( a , i , r );
}
可看博客-快速排序(Lomuto and Hoare 分区) 进一步了解分区的差异
经过分治的思想,平均时间复杂度 $O(nlogn)$,递归需要栈的辅助空间,平均空间复杂度 $O(logn)$。
最坏情况下,每次取点为 min or max,排序过程由二叉树退化成线性树,时间复杂度 $O(n^2)$,空间复杂度 $O(n)$。此时调用树(call tree)变成由 n 个嵌套调用组成的线性连串。
归并排序可分为自顶向下 (递归)和自底向上 (迭代)两种,详见文章
例题-787. 归并排序 | 变式-788. 逆序对的数量
图源: https://www.cnblogs.com/nullzx/p/5968170.html
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
const int N = 1e5 + 10 ;
int a [ N ], t [ N ];
// 自顶向下
void mergesort ( int a [], int l , int r ) {
if ( l >= r ) return ; // 递归出口
int mid = l + r >> 1 ;
mergesort ( a , l , mid );
mergesort ( a , mid + 1 , r );
// 合并两个有序区间 [l, mid] [mid + 1, r]
int i = l , j = mid + 1 , k = 0 ;
while ( i <= mid && j <= r ) {
if ( a [ i ] < a [ j ]) t [ k ++ ] = a [ i ++ ];
else t [ k ++ ] = a [ j ++ ];
}
while ( i <= mid ) t [ k ++ ] = a [ i ++ ];
while ( j <= r ) t [ k ++ ] = a [ j ++ ];
for ( int i = l , k = 0 ; i <= r ; i ++ ) a [ i ] = t [ k ++ ];
}
int main () {
int n ;
cin >> n ;
for ( int i = 0 ; i < n ; i ++ ) cin >> a [ i ];
mergesort ( a , 0 , n - 1 );
for ( int i = 0 ; i < n ; i ++ ) cout << a [ i ] << " " ;
return 0 ;
}
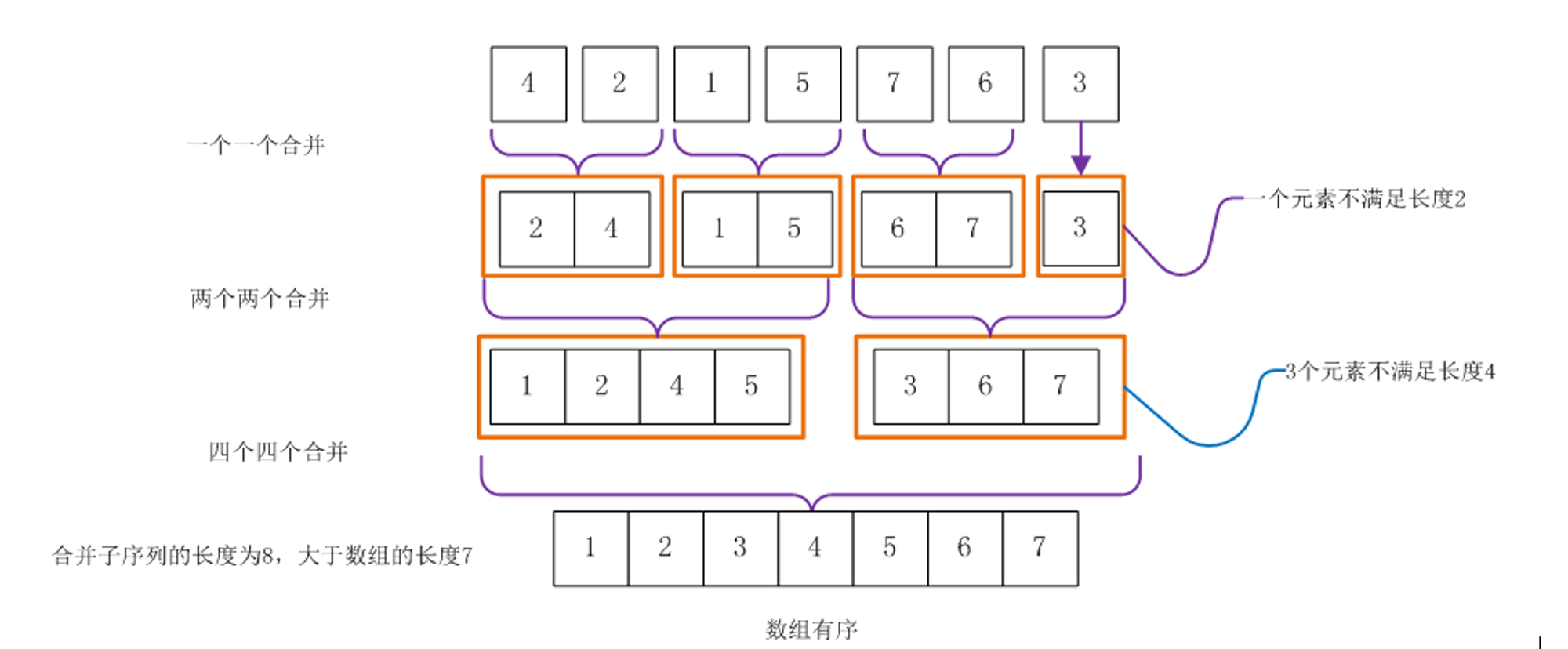
图源: https://www.cnblogs.com/nullzx/p/5968170.html
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
const int N = 1e5 + 10 ;
int a [ N ], t [ N ];
// 合并两个有序区间 [l, mid] [mid + 1, r]
void merge ( int a [], int l , int mid , int r ) {
int i = l , j = mid + 1 , k = 0 ;
while ( i <= mid && j <= r ) {
if ( a [ i ] < a [ j ]) t [ k ++ ] = a [ i ++ ];
else t [ k ++ ] = a [ j ++ ];
}
while ( i <= mid ) t [ k ++ ] = a [ i ++ ];
while ( j <= r ) t [ k ++ ] = a [ j ++ ];
for ( int i = l , k = 0 ; i <= r ; i ++ ) a [ i ] = t [ k ++ ];
}
int main () {
int n ;
cin >> n ;
for ( int i = 0 ; i < n ; i ++ ) cin >> a [ i ];
// 自底向上: 合并的区间长度 1 2 4 8...
for ( int len = 1 ; len < n ; len *= 2 ) {
for ( int k = 0 ; k + len < n ; k += len * 2 ) {
// [k, k + len - 1] | [k + len, k + len*2 - 1]
int l = k ,
mid = k + len - 1 ,
r = min ( k + len * 2 - 1 , n - 1 );
merge ( a , l , mid , r );
}
}
for ( int i = 0 ; i < n ; i ++ ) cout << a [ i ] << " " ;
return 0 ;
}
二分一定有结果,但结果不一定符合题意,需要判断。
例题-789. 数的范围
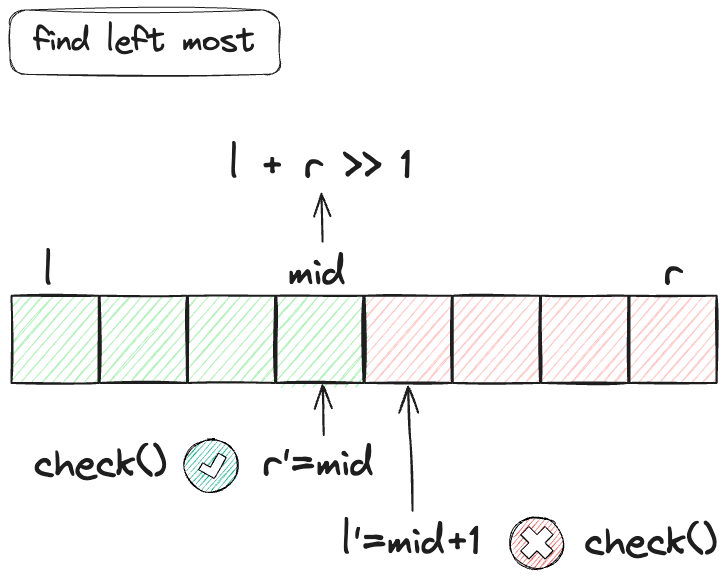
模板一:满足 check() 的最左端的点,区间 $[l, mid], [mid+1, r]$
1
2
3
4
5
6
7
8
9
int l = 0 , r = n - 1 ;
int bsearch_1 ( int l , int r ) {
while ( l < r ) {
int mid = l + r >> 1 ;
if ( check ( mid )) r = mid ;
else l = mid + 1 ;
}
return l ;
}
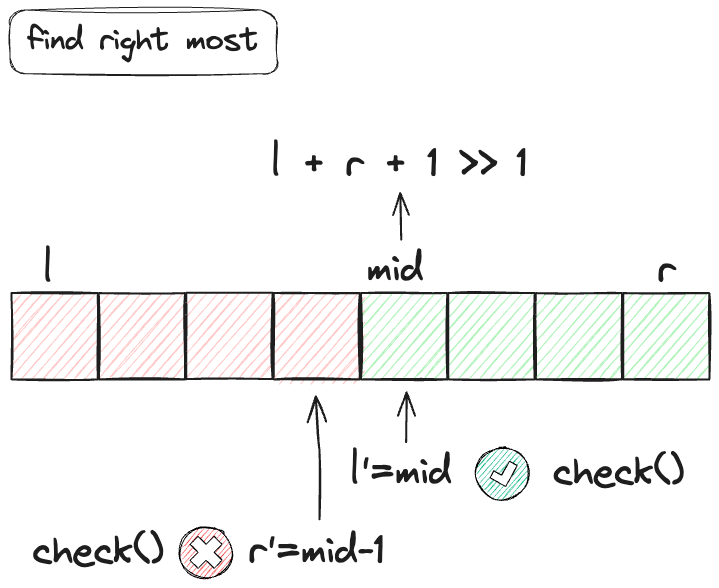
模板二:满足 check() 的最右端的点,区间 $[l, mid-1] [mid, r]$
1
2
3
4
5
6
7
8
9
int l = 0 , r = n - 1 ;
int bsearch_2 ( int l , int r ) {
while ( l < r ) {
int mid = l + r + 1 >> 1 ;
if ( check ( mid )) l = mid ;
else r = mid - 1 ;
}
return l ;
}
例题-790. 数的三次方根
1
2
3
4
5
6
7
8
9
10
11
12
int main () {
double n ;
cin >> n ;
double l = - 100 , r = 100 ;
while ( r - l > 1e-8 ) {
double mid = ( r + l ) / 2 ;
if ( mid * mid * mid >= n ) r = mid ;
else l = mid ;
}
printf ( "%lf" , r ); // 默认6位小数
return 0 ;
}
高精度一般数据范围如下,直接数组模拟运算即可,更大的数需要压位算法 (暂不考虑)。
$A + B$:两个大整数相加,$len(A), len(B) ≤ 10^6$
$A - B$:两个大整数相减,$len(A), len(B) ≤ 10^6$
$A * b$:大整数乘小整数,$len(A) ≤ 10^6, b ≤ 10^9$
$A / b$:大整数除小整数,$len(A) ≤ 10^6, b ≤ 10^9$
一般数组下标 0 存储大整数的个位,方便进位时直接在数组后添加
A + B 例题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <iostream>
#include <vector>
using namespace std ;
// C = A + B, A >= 0, B >= 0
vector < int > add ( vector < int > & A , vector < int > & B ) {
vector < int > C ;
int t = 0 ; // 进位
for ( int i = 0 ; i < A . size () || i < B . size (); i ++ ) {
if ( i < A . size ()) t += A [ i ];
if ( i < B . size ()) t += B [ i ];
C . push_back ( t % 10 );
t /= 10 ;
}
if ( t ) C . push_back ( t );
return C ;
}
int main () {
string a , b ;
cin >> a >> b ;
vector < int > A , B ;
for ( int i = a . size () - 1 ; i >= 0 ; i -- ) A . push_back ( a [ i ] - '0' );
for ( int i = b . size () - 1 ; i >= 0 ; i -- ) B . push_back ( b [ i ] - '0' );
auto C = add ( A , B );
for ( int i = C . size () - 1 ; i >= 0 ; i -- ) cout << C [ i ];
return 0 ;
}
A - B 例题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
// 判断 A >= B
bool cmp ( vector < int > & A , vector < int > & B ) {
if ( A . size () != B . size ()) {
return A . size () > B . size ();
}
for ( int i = A . size () - 1 ; i >= 0 ; i -- ) {
if ( A [ i ] != B [ i ]) {
return A [ i ] > B [ i ];
}
}
return true ; // A == B
}
// C = A - B, 满足A >= B, A >= 0, B >= 0
vector < int > sub ( vector < int > & A , vector < int > & B ) {
vector < int > C ;
int t = 0 ; // 借位
for ( int i = 0 ; i < A . size (); i ++ ) {
// t = a - b - t;
t = A [ i ] - t ;
if ( i < B . size ()) {
t -= B [ i ];
}
// t >= 0 => t, t < 0 => t + 10
C . push_back (( t + 10 ) % 10 );
if ( t < 0 ) t = 1 ; // 有借位
else t = 0 ; // 无借位
}
// 去除前导 0
while ( C . size () > 1 && C . back () == 0 ) C . pop_back ();
return C ;
}
int main () {
string a , b ;
cin >> a >> b ;
vector < int > A , B ;
for ( int i = a . size () - 1 ; i >= 0 ; i -- ) A . push_back ( a [ i ] - '0' );
for ( int i = b . size () - 1 ; i >= 0 ; i -- ) B . push_back ( b [ i ] - '0' );
if ( cmp ( A , B )) {
// A >= B
auto C = sub ( A , B );
for ( int i = C . size () - 1 ; i >= 0 ; i -- ) cout << C [ i ];
} else {
// A < B
auto C = sub ( B , A );
cout << '-' ;
for ( int i = C . size () - 1 ; i >= 0 ; i -- ) cout << C [ i ];
}
return 0 ;
}
A * b 例题
把 b 看成一个整体,和 A 的每一位去做乘法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// C = A * b, A >= 0, b >= 0
vector < int > mul ( vector < int > & A , int b ) {
vector < int > C ;
int t = 0 ;
for ( int i = 0 ; i < A . size (); i ++ ) {
t += A [ i ] * b ;
C . push_back ( t % 10 );
t /= 10 ;
}
while ( t ) {
C . push_back ( t % 10 );
t /= 10 ;
}
// 去除前导 0(b = 0 的情况)
while ( C . size () > 1 && C . back () == 0 ) C . pop_back ();
return C ;
}
int main () {
string a ;
int b ;
cin >> a >> b ;
vector < int > A ;
for ( int i = a . size () - 1 ; i >= 0 ; i -- ) A . push_back ( a [ i ] - '0' );
auto C = mul ( A , b );
for ( int i = C . size () - 1 ; i >= 0 ; i -- ) cout << C [ i ];
return 0 ;
}
A / b 例题
模拟手动除法,从最高位除起,依次做商和取余。每一轮的余数,乘以10,加上下一位的数,作为下一轮的被除数。
注意:在除法中结果数组 C 第0位存高位,而不是低位,所以最后做一个逆序翻转的统一处理。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// A / b = C ... r, A >= 0, b > 0
vector < int > div ( vector < int > & A , int b , int & r ) {
vector < int > C ;
// 高位开始除法
r = 0 ; // 余数
for ( int i = A . size () - 1 ; i >= 0 ; i -- ) {
r = r * 10 + A [ i ];
C . push_back ( r / b );
r %= b ;
}
// 逆序,使数组从低位开始
reverse ( C . begin (), C . end ());
// 去除前导 0
while ( C . size () > 1 && C . back () == 0 ) C . pop_back ();
return C ;
}
int main () {
string a ;
int b ;
cin >> a >> b ;
vector < int > A ;
for ( int i = a . size () - 1 ; i >= 0 ; i -- ) A . push_back ( a [ i ] - '0' );
int r = 0 ;
auto C = div ( A , b , r );
for ( int i = C . size () - 1 ; i >= 0 ; i -- ) cout << C [ i ];
cout << '\n' << r ;
return 0 ;
}
不需要去除前导 0 的写法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
vector < int > div ( vector < int >& A , int b ) {
vector < int > C ;
int r = 0 ;
bool first = true ;
for ( int i = A . size () - 1 ; i >= 0 ; i -- ) {
r = r * 10 + A [ i ];
int x = r / b ;
if ( ! first || x ) {
first = false ;
C . push_back ( x );
}
r %= b ;
}
reverse ( C . begin (), C . end ());
return C ;
}
1
2
3
4
5
6
7
8
9
10
11
const int N = 100010 ;
int s [ N ];
for ( int i = 1 ; i <= n ; i ++ ) { // 下标从 1 开始
cin >> s [ i ];
s [ i ] += s [ i - 1 ];
}
int get ( int l , int r ) {
return s [ r ] - s [ l - 1 ];
}
扩展运算 1:异或
1
2
3
4
5
6
7
8
// 异或 a1 ^ a2 ^ ... ^ an
for ( int i = 1 ; i <= n ; i ++ ) {
s [ i ] ^= s [ i - 1 ];
}
int get ( int l , int r ) {
return s [ r ] ^ s [ l - 1 ];
}
扩展运算 2:或
1
2
3
4
5
6
7
8
9
10
11
12
13
// 或 a1 | a2 | ... | an
const int N = 1e5 + 10 , MAXBIT = 30 ;
int pre [ N ][ MAXBIT + 1 ]; // 按位 前缀和数组
for ( int i = 1 ; i <= n ; i ++ ) {
for ( int j = 0 ; j <= MAXBIT ; j ++ ) {
pre [ i ][ j ] = pre [ i - 1 ][ j ] + (( a [ i ] >> j ) & 1 );
}
}
int get ( int l , int r , int bit ) {
return pre [ r ][ bit ] - pre [ l - 1 ][ bit ];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
const int N = 1010 ;
int a [ N ][ N ], s [ N ][ N ];
int n , m , q ;
int main () {
cin >> n >> m >> q ;
for ( int i = 1 ; i <= n ; i ++ )
for ( int j = 1 ; j <= m ; j ++ )
cin >> a [ i ][ j ];
for ( int i = 1 ; i <= n ; i ++ )
for ( int j = 1 ; j <= m ; j ++ )
s [ i ][ j ] = s [ i - 1 ][ j ] + s [ i ][ j - 1 ] - s [ i - 1 ][ j - 1 ] + a [ i ][ j ];
while ( q -- ) {
int x1 , x2 , y1 , y2 ;
cin >> x1 >> y1 >> x2 >> y2 ;
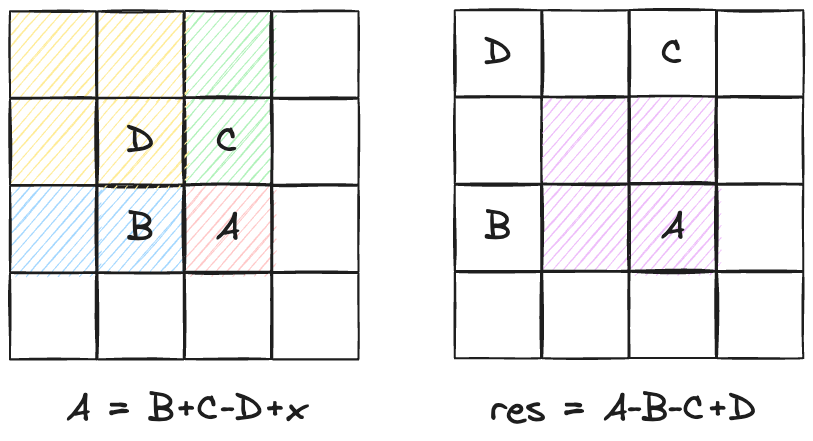
int res = s [ x2 ][ y2 ] - s [ x1 - 1 ][ y2 ] - s [ x2 ][ y1 - 1 ] + s [ x1 - 1 ][ y1 - 1 ];
cout << res << '\n' ;
}
return 0 ;
}
差分是前缀和的逆操作,对差分数组进行前缀求和得到原数组。
例题 :
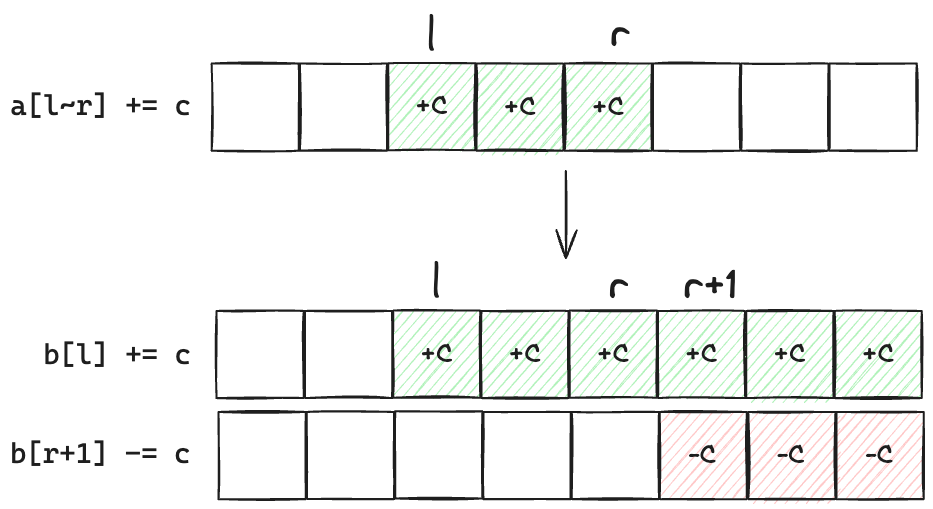
将序列中 $[l,r]$ 之间的每个数加上 c,输出操作后的序列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
const int N = 100010 ;
int a [ N ]; // 原数组
int b [ N ]; // 差分数组
void insert ( int l , int r , int c ) {
b [ l ] += c ;
b [ r + 1 ] -= c ;
}
int main () {
int n , m ;
cin >> n >> m ;
// 原数组
for ( int i = 1 ; i <= n ; i ++ ) cin >> a [ i ];
// 差分数组,[i, i] 每个数增加 a[i]
for ( int i = 1 ; i <= n ; i ++ ) insert ( i , i , a [ i ]);
while ( m -- ) {
int l , r , c ;
cin >> l >> r >> c ;
insert ( l , r , c );
}
// 差分数组求前缀和得到实际值
for ( int i = 1 ; i <= n ; i ++ ) b [ i ] += b [ i - 1 ];
for ( int i = 1 ; i <= n ; i ++ ) cout << b [ i ] << ' ' ;
return 0 ;
}
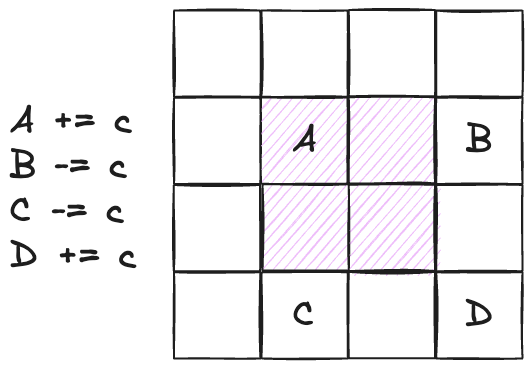
二维差分-例题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
const int N = 1010 ;
int a [ N ][ N ], b [ N ][ N ];
void insert ( int x1 , int y1 , int x2 , int y2 , int c ) {
b [ x1 ][ y1 ] += c ;
b [ x2 + 1 ][ y1 ] -= c ;
b [ x1 ][ y2 + 1 ] -= c ;
b [ x2 + 1 ][ y2 + 1 ] += c ;
}
int main () {
int n , m , q ;
cin >> n >> m >> q ;
for ( int i = 1 ; i <= n ; i ++ ) {
for ( int j = 1 ; j <= m ; j ++ ) {
cin >> a [ i ][ j ];
insert ( i , j , i , j , a [ i ][ j ]);
}
}
while ( q -- ) {
int x1 , y1 , x2 , y2 , c ;
cin >> x1 >> y1 >> x2 >> y2 >> c ;
insert ( x1 , y1 , x2 , y2 , c );
}
// 差分数组求前缀和得到实际值
for ( int i = 1 ; i <= n ; i ++ )
for ( int j = 1 ; j <= m ; j ++ )
b [ i ][ j ] = b [ i - 1 ][ j ] + b [ i ][ j - 1 ] - b [ i - 1 ][ j - 1 ] + b [ i ][ j ];
// 输出打印
for ( int i = 1 ; i <= n ; i ++ ) {
for ( int j = 1 ; j <= m ; j ++ ) {
cout << b [ i ][ j ] << ' ' ;
}
puts ( "" );
}
return 0 ;
}
核心思想是将朴素的 $O(n^2)$ 优化到 $O(n)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// O(n^2)
for ( int i = 0 ; i < n ; i ++ ) {
for ( int j = 0 ; j < n ; j ++ ) {
//...
}
//...
}
// O(n) 双指针优化
for ( int i = 0 , j = 0 ; i < n ; i ++ ) {
while ( i < j && check ( i , j )){
j ++ ;
//...
}
//...
}
最长连续不重复子序列 :找出最长的不包含重复的数的连续区间,输出它的长度
1
2
3
4
5
6
7
8
9
10
11
int res = 0 ;
// two pointers: [j, i] 先不断扩张右端点
for ( int i = 0 , j = 0 ; i < n ; i ++ ) {
cnt [ a [ i ]] ++ ;
// 当出现重复数字,左端右移,直到剔除新加入的重复元素
while ( cnt [ a [ i ]] > 1 ) {
cnt [ a [ j ]] -- ;
j ++ ;
}
res = max ( res , i - j + 1 );
}
数组元素的目标和 :两个升序数组 A 和 B,目标值 x,求出满足 $A[i]+B[j]=x$ 的数对 $(i,j)$
利用单调性,对位置 i 求最靠右的位置 j 使得 $a[i] + b[j] ≤ x$
1
2
3
4
5
6
7
8
// 指针分在两端
for ( int i = 0 , j = m - 1 ; i < n ; i ++ ) {
while ( j >= 0 && a [ i ] + b [ j ] > x ) j -- ; // 当前的 b[j] 对于 a[i] 之后的数没有意义了
if ( a [ i ] + b [ j ] == x ) {
cout << i << ' ' << j ;
break ;
}
}
判断子序列 :子序列是指序列的一部分项按原有次序排列而得的序列
1
2
3
4
5
6
7
8
int i = 0 , j = 0 ;
while ( i < n && j < m ) {
if ( a [ i ] == b [ j ]) i ++ ;
j ++ ;
}
if ( i < n ) cout << "No" ;
else cout << "Yes" ;
其他双指针题目:
Leetcode - 209. 长度最小的子数组 :数组元素都是正数 ,求满足总和 $>=k$ 的最短连续子数组。
Leetcdoe - 862. 和至少为 K 的最短子数组 :数组元素存在负数 ,求满足总和 $>=k$ 的最短连续子数组,需要额外使用单调队列。
基本位运算
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 二进制表示第 k 位
x >> k & 1
// 返回二进制表示中最右侧的 1 后的二进制 (100..00)
// lowbit(10100) = 100
int lowbit ( int x ) {
return x & - x ; // = x & (~x + 1) 因为 -x = ~x + 1
}
// 将二进制表示最右侧的 1 置 0
x ^= x & - x ; // (x & -x) 得到最右侧 1(0..010..0),异或取反
x -= x & - x ;
x &= x - 1 ; // 最优
// 判断是否为 2 的整数次方 (100..00)
// 二进制中有且仅有一位是 1,将其最右侧的 1 置 0 后等于 0
x & ( x - 1 ) == 0
统计 n 的二进制表示中 1 的个数
1
2
3
4
5
6
7
8
9
10
class Solution {
public :
int hammingWeight ( uint32_t n ) {
int cnt = 0 ;
for ( uint32_t i = n ; i ; i -= i & - i ) {
cnt ++ ;
}
return cnt ;
}
};
判断整数 m 的二进制需要改变多少位才能变为 n
1
2
3
4
5
// 计算 m 与 n 的异或的二进制中 1 的个数
int cnt = 0 ;
x = m ^ n ;
for ( int i = x ; i ; i -= i & - i ) cnt ++ ;
cout << cnt ;
位运算实现加法
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public :
int add ( int a , int b ) {
while ( b ) {
// 记录进位部分
int t = ( unsigned int )( a & b ) << 1 ;
a = a ^ b ;
b = t ;
}
return a ;
}
};
注意位移运算不要有负数参与
The left shift and right shift operators should not be used for negative numbers. The result of is undefined behaviour if any of the operands is a negative number. For example results of both -1 « 1 and 1 « -1 is undefined.
离散化的本质是映射,数组元素值域很大但个数很少时,可以通过离散化对“稀疏数组”进行压缩,减少对空间的需求,也减少计算量。如将有序数组 $[1, 3, 100, 2000, 500000]$ 映射为 $[0, 1, 2, 3, 4]$。
为什么要离散化?
直接用数组存储值会有问题:值域为 $[0, 10^9]$ 时开一个 $10^9$ 大小的数组太浪费也会爆内存,且无法直接存储负数。
哈希表同样有 $O(1)$ 的下标取值效率,存储上不会有问题,但计算操作上会带来问题:哈希表不能像离散化那样缩小数组的空间,也不能排序,导致可能需要从 $-10^9$ 到 $10^9$ 去遍历判断的 $O(n)$ 操作。
离散化的要点:
原数组若有重复元素,可能需要去重
映射关系:如何将不连续的点映射到连续的数组下标,当原数组有序时,可通过二分查找 算出其离散化后的值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
vector < int > indexes ; // 待离散化的数组,即所有需要映射的点
// indexes 去重
sort ( indexes . begin (), indexes . end ());
indexes . erase ( unique ( indexes . begin (), indexes . end ()), indexes . end ());
// 二分查找原值映射后的下标
int find ( int x ) {
int l = 0 , r = indexes . size () - 1 ;
while ( l < r ) {
int mid = l + r >> 1 ;
if ( indexes [ mid ] >= x ) r = mid ;
else l = mid + 1 ;
}
return r ;
}
例题:802. 区间和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
typedef pair < int , int > PII ;
const int N = 3e5 + 10 ; // n + 2*m 添加映射一个点 查询映射两个点
int a [ N ]; // 映射后的数组下标对应的数值,下标从 1 开始,方便前缀和
vector < int > indexes ; // 所有需要映射的点
vector < PII > add , query ; // 添加 和 查询的操作数
// 二分查找值映射后的下标
int find ( int x ) {
int l = 0 , r = indexes . size () - 1 ;
while ( l < r ) {
int mid = l + r >> 1 ;
if ( indexes [ mid ] >= x ) r = mid ;
else l = mid + 1 ;
}
return r + 1 ; // 下标从 1 开始,方便前缀和
}
int main () {
int n , m ;
cin >> n >> m ;
// 存下添加值,记录需要映射的点
for ( int i = 0 ; i < n ; i ++ ) {
int x , c ;
cin >> x >> c ;
add . push_back ({ x , c });
indexes . push_back ( x );
}
// 存下查询值,记录需要映射的点
for ( int i = 0 ; i < m ; i ++ ) {
int l , r ;
cin >> l >> r ;
query . push_back ({ l , r });
// 查询之前没有映射的点
indexes . push_back ( l );
indexes . push_back ( r );
}
// indexes 去重
sort ( indexes . begin (), indexes . end ());
indexes . erase ( unique ( indexes . begin (), indexes . end ()), indexes . end ());
// 执行添加操作
for ( auto op : add ) {
int x = find ( op . first );
a [ x ] += op . second ;
}
// 计算前缀和
for ( int i = 1 ; i <= indexes . size (); i ++ ) {
a [ i ] += a [ i - 1 ];
}
// 执行查询
for ( auto q : query ) {
int l = find ( q . first ), r = find ( q . second );
cout << a [ r ] - a [ l - 1 ] << '\n' ;
}
return 0 ;
}
约数之和 :
自然数 A 和 B,S 是 $A^B$ 的所有约数之和,求 S mod 9901 的值
计算 ${p_i}^0 + {p_i}^1 + … + {p_i}^{\alpha_i*B}$ 可使用递推法优化到 $O(logn)$
项数为偶 $(k + 1) % 2 == 0$:
$sum(p, k) = p^0 + p^1 + … + p^k$
$=(p^0 + … + p^{k/2})+(p^{k/2+1} + … + p^k)$
$=(p^0 + … + p^{k/2})+p^{k/2+1}*(p^0 + … + p^{k/2})$
$= (1 + p^{k/2+1}) * sum(p, k/2)$
项数为奇 $(k + 1) % 2 == 1$:
$sum(p, k) = p * sum(p, k - 1) + p^0= p * sum(p, k - 1) + 1$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 快速幂
int qmi ( int a , int k ) {
int res = 1 ;
a %= mod ;
while ( k ) {
if ( k & 1 ) res = res * a % mod ;
a = a * a % mod ;
k >>= 1 ;
}
return res ;
}
// p^0 + p^1 +...+ p^k
int sum ( int p , int k ) {
if ( k == 0 ) return 1 ;
// 偶数项可以均分为两部分
if (( k + 1 ) % 2 == 0 ) {
// sum(p, k) = (1 + p^{k/2+1}) * sum(p, k/2)
return ( 1 + qmi ( p , k / 2 + 1 )) * sum ( p , k / 2 ) % mod ; // qmi 已包含 mod,不用添加额外 mod
} else {
// 奇数项转换成偶数项
return ( p % mod * sum ( p , k - 1 ) + 1 ) % mod ; // 额外 mod 防止溢出
}
}
分形之城 :计算规律变换后的坐标点距离
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <iostream>
#include <cmath>
using namespace std ;
typedef long long LL ;
struct Point {
LL x , y ;
};
// 计算等级 n 序号 a(>=0) 的坐标
Point calc ( int n , LL a ) {
if ( n == 0 ) return { 0 , 0 };
LL len = 1ll << ( n - 1 ); // 2^(n-1) 象限边长
LL block = 1ll << ( 2 * n - 2 ); // 4^(n-1) 象限容量
// 上一等级的坐标
Point p = calc ( n - 1 , a % block );
LL x = p . x , y = p . y ;
// 变换至当前坐标(以中心点为原点)
int idx = a / block ; // 判断象限
if ( idx == 0 ) return { - y - len , - x + len }; // 沿 y=-x 翻转 + 平移
else if ( idx == 1 ) return { x + len , y + len };
else if ( idx == 2 ) return { x + len , y - len };
else return { y - len , x - len }; // 沿 y=x 翻转 + 平移
}
int main () {
int N ;
cin >> N ;
while ( N -- ) {
LL n , a , b ;
cin >> n >> a >> b ;
Point p1 = calc ( n , a - 1 );
Point p2 = calc ( n , b - 1 );
double dx = p1 . x - p2 . x ;
double dy = p1 . y - p2 . y ;
// 以中心点为原点,实际 len 减半
printf ( "%.0lf \n " , sqrt ( dx * dx + dy * dy ) * 10 / 2 );
}
return 0 ;
}
RMQ(Range Minimum/Maximum Query) 表示区间最大(最小)值查询:是一个快速求区间最值的离线算法 (源数据不能修改),预处理时间复杂度 $O(nlog(n))$,单次查询 $O(1)$。例题
$F[i, j]$ 表示从第$i$个数起连续$2^j$个数中的最大值,则可预处理所有$F[i, j]$
查询时:
$query(l, r) = max(f[l][k], f[r - 2^k + 1][k])$,其中 $k=log_2n$ 下取整
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <iostream>
#include <cmath>
using namespace std ;
const int N = 2e5 + 10 , M = 18 ; // 2*10^5->2^18 元素数量
int a [ N ];
int f [ N ][ M ];
int query ( int l , int r ) {
int len = r - l + 1 ;
int k = log ( len ) / log ( 2 ); // log2(len) 下取整 => 2^k <= len
// [l, l + 2^k - 1] ... r]
// [l ... [r - 2^k + 1, r]
return max ( f [ l ][ k ], f [ r - ( 1 << k ) + 1 ][ k ]);
}
int main () {
int n , t ;
cin >> n ;
for ( int i = 1 ; i <= n ; i ++ ) cin >> a [ i ];
// 预处理
for ( int j = 0 ; j < M ; j ++ ) {
// [i, i + 2^j - 1]
for ( int i = 1 ; i + ( 1 << j ) - 1 <= n ; i ++ ) {
if ( j == 0 ) {
f [ i ][ j ] = a [ i ];
} else {
f [ i ][ j ] = max ( f [ i ][ j - 1 ], f [ i + ( 1 << ( j - 1 ))][ j - 1 ]);
}
}
}
cin >> t ;
while ( t -- ) {
int l , r ;
cin >> l >> r ;
cout << query ( l , r ) << endl ;
}
return 0 ;
}