链表
结构体指针
链表的第一种表达方式是直接使用指针指向下一节点,节点内容使用结构体包裹。这一方式可读性强,但 newNode() 构造非常慢,一般在面试中为了易读而使用,在笔试时为了性能而一般不用。
单链表:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
struct ListNode {
int val;
ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};
// 添加元素 - 尾插法
void LinkPushBack(LinkNode* head, int x) {
LinkNode* newNode = LinkNode(x);
if (head == NULL) {
head = newNode;
return;
}
LinkNode* pcur = head;
while (pcur->next) {
pcur = pcur -> next;
}
pcur->next = newNode;
}
|
数组模拟
链表的另一种表达方式是使用数组模拟链表,不使用结构体,各节点内容单独使用数组。常用于表示树、图的邻接表,代码书写简洁,运行速度快。
单链表 例题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
int e[N]; // node's value
int ne[N]; // node's next pointer
int head = -1, idx = 0;
// 向链表头插入一个数 x
void addHead(int x) {
e[idx] = x;
ne[idx] = head;
head = idx;
idx++;
}
// 在第 k 个插入的数后面插入一个数 x(k > 0)
void insert(int k, int x) {
e[idx] = x;
ne[idx] = ne[k];
ne[k] = idx;
idx++;
}
// 删除第 k 个插入的数后面的数(k > 0)
void remove(int k) {
ne[k] = ne[ne[k]];
}
// 遍历输出
for (int i = head; i != -1; i = ne[i]) {
cout << e[i] << " ";
}
|
双向链表(用于问题优化)例题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
int e[N], l[N], r[N], idx;
void init() {
// 两个特殊节点 0: head 1: tail
r[0] = 1;
l[1] = 0;
idx = 2;
}
// add(k, x) 在第 k 个插入的数 右侧 插入一个数 x
// add(l[k], x) 在第 k 个插入的数 左侧 插入一个数 x
void add(int k, int x) {
e[idx] = x, l[idx] = k, r[idx] = r[k];
l[r[k]] = idx;
r[k] = idx;
idx++;
}
// 删除第 k 个插入的数
void removeK(int k) {
r[l[k]] = r[k];
l[r[k]] = l[k];
}
|
栈 & 队列
数组模拟栈:先进后出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
const int N = 1e5+10;
int stk[N], tt = -1;
void push(int x) {
stk[++tt] = x;
}
void pop() {
--tt;
}
bool empty() {
return tt < 0;
}
int query() {
return stk[tt];
}
|
数组模拟队列(顺序队列):先进先出,在队尾入,在队头出
当数组有空闲空间,但无法入队时,需要做一次数据搬移操作(链式队列或循环队列没有此问题)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
const int N = 1e5+10;
int q[N], hh = 0, tt = -1; // [head, tail]
void push(int x) {
q[++tt] = x;
}
void pop() {
hh++;
}
int query() {
return q[hh];
}
int queryAndPop {
return q[hh++];
}
bool empty() {
return tt < hh; // tt >= hh is not empty
}
|
单调栈 & 单调队列
单调栈和单调队列的问题:
先想暴力怎么做,再考虑把没有用的元素删掉,再看有没有单调性,有单调性的话再看怎么优化
单调栈 例题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
const int N = 1e5 + 10;
int stk[N], tt = -1;
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
int x;
cin >> x;
while (tt >= 0 && x <= stk[tt]) tt--;
if (tt < 0) cout << -1 << " ";
else cout << stk[tt] << " ";
stk[++tt] = x;
}
return 0;
}
|
单调队列 例题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
// 求滑动窗口中的最小值
const int N = 1e6+10;
int a[N];
int main() {
int n, k;
cin >> n >> k;
for (int i = 0; i < n; i++) cin >> a[i];
// MIN
deque<int> deq; // 双向队列存下标
for (int i = 0; i < n; i++) {
// 判断队头是否滑出窗口
if (!deq.empty() && i - k + 1 > deq.front()) deq.pop_front();
while(!deq.empty() && a[deq.back()] >= a[i]) deq.pop_back();
deq.push_back(i);
if (i >= k - 1) cout << a[deq.front()] << ' ';
}
cout << '\n';
return 0;
}
|
KMP
KMP 用于在文本串中快速查找一个模式串的出现位置
例题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
#include <iostream>
using namespace std;
const int M = 1e6+10, N = 1e5+10;
char s[M], p[N]; // 主串 模式串,下标从 1 开始,可简化代码
int ne[N]; // 针对模式串 P 而言,记录前缀和后缀相同的最长长度
int main() {
int n, m;
cin >> n >> p + 1 >> m >> s + 1;
// get next, ne[1~n]
// ne[j] = [1~j] 最长 相同 前-后缀
// ne[1] = 0
for (int i = 2, j = 0; i <= n; i++) {
while (j && p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) j++;
ne[i] = j;
}
for (int i = 1; i <= n; i++) cout << ne[i] << " ";
cout << "\n";
// kmp
for (int i = 1, j = 0; i <= m; i++) { // i->主串 j->pattern
while (j && s[i] != p[j + 1]) j = ne[j];
if(s[i] == p[j + 1]) j++; // s[i] vs. p[j + 1]
// 完全匹配 pattern
if (j == n) {
cout << i - n << " ";
j = ne[j]; // 继续匹配下一个
}
}
return 0;
}
|
堆
堆是完全二叉树,小根堆中每个节点的值小于两个子节点,建堆时间复杂度O(n)。堆常用于求 TopK,优先队列,堆排序。
基础 down 与 up 操作实现(数组下标从 1 开始):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
void down(int u) {
int l = u * 2, r = u * 2 + 1; // 下标从 1 开始对应的左右儿子
int t = u; // t 用于记录值最小的节点
if (l <= hsize && h[l] < h[t]) t = l;
if (r <= hsize && h[r] < h[t]) t = r;
if (t != u) {
swap(h[u], h[t]);
down(t);
}
}
// down 的迭代写法
void down_iter(int u) {
int i = u;
while (i < hsize) {
int t = i;
int l = 2 * i + 1, r = 2 * i + 2;
if (l < hsize && h[l] > h[t]) t = l;
if (r < hsize && h[r] > h[t]) t = r;
if (t == i) break;
swap(h[i], h[t]);
i = t;
}
}
void up(int u) {
while (u / 2 && h[u / 2] > h[u]) {
swap(u / 2, u);
u /= 2;
}
}
|
建堆的两种方式:
- HeapInsert (up) $O(nlogn)$:假定我们事先不知道有多少个元素,通过不断往堆里面插入元素进行调整来构建堆
- Heapify (down) $O(n)$:从最后一个非叶子节点一直到根结点进行堆化的调整
1
2
3
4
5
6
7
8
9
|
// 从第一个节点开始遍历,直到最后一个节点,向上调整
for (int i = 1; i <= n; i++) {
up(i);
}
// 从最后一个非叶节点开始,不断向下调整
for (int i = n / 2; i; i--) {
down(i);
}
|
堆排序 例题 | LeetCode 912. 排序数组
1)使用小根堆直接输出顺序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
const int N = 1e5+10;
int h[N], hsize; // h 数组下标从 1 开始
// 建堆,下标从 1 开始
for (int i = 1; i <= n; i++) cin >> h[i];
hsize = n;
for (int i = n / 2; i; i--) down(i);
// 依次输出前 M 小的数
while (m--) {
// 输出当前最小值
cout << h[1] << ' ';
// 删去当前最小值(把最后一个数放在第一的位置 hsize--)再 down(1) 后得到新的最小值
h[1] = h[hsize];
hsize--;
down(1);
}
|
2)使用大根堆对原数组排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
class Solution {
public:
vector<int> sortArray(vector<int>& nums) {
heapSort(nums);
return nums;
}
void heapSort(vector<int>& nums) {
int n = nums.size();
// 建大根堆
for (int i = n / 2 - 1; i >= 0; i--) {
down(nums, i, n);
}
// 堆排序
for (int i = n - 1; i > 0; i--) {
// 将堆顶元素弹出,和堆的末尾元素交换,此时 [i, n-1] 为排序后的区间,[0, i-1] 为堆的元素范围
swap(nums[0], nums[i]);
down(nums, 0, i); // 维护堆
}
}
void down(vector<int>& nums, int u, int hsize) {
int n = nums.size();
int t = u, l = u * 2 + 1, r = u * 2 + 2;
if (l < hsize && nums[l] > nums[t]) t = l;
if (r < hsize && nums[r] > nums[t]) t = r;
if (t != u) {
swap(nums[t], nums[u]);
down(nums, t, hsize);
}
}
};
|
堆的完全模拟(维护堆的坐标映射-不常用)
例题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
|
const int N = 1e5+10;
int h[N], hsize; // h 数组下标从 1 开始
int ph[N]; // ph[k] = j; 第 k 个插入的数的下标 j,直接使用
int hp[N]; // hp[j] = k; 下标为 j 的数是第 k 个插入的,维护 ph[] 需要使用
void heap_swap(int a, int b) {
swap(ph[hp[a]], ph[hp[b]]);
swap(hp[a], hp[b]);
swap(h[a], h[b]);
}
// down 递归(堆的初始排序使用,顺序打印对根节点使用 down(1),删除更新可能使用)
void down(int u) {
int l = u * 2, r = u * 2 + 1; // 下标从 1 开始对应的左右儿子
int t = u; // t 用于记录值最小的节点
if (l <= hsize && h[l] < h[t]) t = l;
if (r <= hsize && h[r] < h[t]) t = r;
if (t != u) {
heap_swap(u, t);
down(t);
}
}
// up 非递归(建堆完成后,添加一个新元素使用 up(++hsize),删除更新可能使用)
void up(int u) {
while (u / 2 && h[u / 2] > h[u]) {
heap_swap(u / 2, u);
u /= 2;
}
}
if (op == "I") { // insert
cin >> x;
idx++, hsize++;
ph[idx] = hsize;
hp[hsize] = idx;
h[hsize] = x;
up(hsize);
} else if (op == "PM") { // print minus
cout << h[1] << '\n';
} else if (op == "DM") { // delete minus
heap_swap(1, hsize);
hsize--;
down(1);
} else if (op == "D") { // delete k_th
cin >> k;
k = ph[k];
heap_swap(k, hsize);
hsize--;
down(k), up(k); // 最多执行一个
} else { // assign k_th = x
cin >> k >> x;
k = ph[k];
h[k] = x;
down(k), up(k); // 最多执行一个
}
|
哈希表
哈希表的操作一般只是插入和查询,很少删除,实际删除也是打标签 flag = false。
Mod 选尽可能大的质数,且离 2 的整次幂尽可能远,保证冲突最小。
哈希冲突
解决哈希冲突的算法有两种:拉链法、开放寻址法
例题
拉链法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
const int N = 100003; // 大于 1e5 的第一个质数
int h[N]; // 存储节点的下标,拉链槽,h[k] 指向 hash=k 的链表头
int e[N], ne[N], idx = 0; // 链表
// 初始化链表头为 -1
memset(h, -1, sizeof h);
void insert(int x) {
int k = (x % N + N) % N; // 保证 k 为正数
e[idx] = x; // 新分配一个节点
ne[idx] = h[k]; // 新节点插在链表头前
h[k] = idx++; // 更新头结点
}
bool query(int x) {
int k = (x % N + N) % N;
for (int i = h[k]; i != -1; i = ne[i]) {
if (e[i] == x) return true;
}
return false;
}
|
开放寻址法(线性探测):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
const int N = 200003; // Mod 一般是 N 的 2~3 倍
const int null = 0x3f3f3f3f;
int h[N];
// 初始化链表头为 null (> 1e9)
memset(h, 0x3f, sizeof h);
// 返回找到的 or 没找到可插入的地址
int search(int x) {
int k = (x % N + N) % N;
while (h[k] != null && h[k] != x) {
k++;
if (k == N) k = 0; // 循环
}
return k;
}
int t = search(x);
// 插入
h[t] = x;
// 查询
if (h[t] != null) puts("Yes");
else puts("No");
|
字符串前缀哈希
字符串前缀哈希用于快速求解任意的子串的哈希值,可以快速判断两个字符串是否相等。
例题
模式匹配需要至少 $O(n)$,而字符串哈希只需要 $O(1)$)
字符串哈希是把字符串变成一个 p 进制数字(哈希值),实现不同的字符串映射到不同的数字的算法。
即对字符串 $x_1x_2x_3⋯x_{n−1}x_n$,采用字符的 ascii 码乘上 P 的次方来计算哈希值,映射公式如下:
$(x_1×P^{n−1}+x_2×P^{n−2}+⋯+x_{n−1}×P^1+x_n×P^0) \bmod Q$
- 字符不能映射为 0,否则哈希值无法区分字符串,比如 A,AA,AAA 皆为0
- 设置以下参数,则默认不存在冲突
- P = 131 or 13331
- Q = $2^{64}$,直接用 ULL 存哈希结果,达到取模 $2^{64}$ 的效果
朴素的哈希方法每次需要重新计算,当子串查询太多则会导致超时,这里可以预处理哈希值前缀和数组,空间换时间:
-
前缀和公式 $h[i+1]=h[i]×P+s[i] i∈[0,n−1]$,h为前缀和数组,s为字符串数组
-
区间和公式 $h[l,r]=h[r]−h[l−1]×P[r−l+1]$
区间和公式举例,求 ABCDE 中 $DE[4,5]$ 的哈希值 $h[5] - h[3] * P^2$,含义如下:
$ABC$ 经过 $* P^2$ 操作变为 $ABC00$,$ABCDE - ABC00$ 就得到 DE 的哈希值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
#include <iostream>
using namespace std;
typedef unsigned long long ULL;
const int N = 1e5+10, P = 131;
ULL h[N]; // 字符串前缀哈希
ULL p[N]; // P 的幂
// [3, 6] -> h[6]-h[2]*p[4]
ULL get(int l, int r) {
return h[r] - h[l - 1] * p[r - l + 1];
}
int main() {
int n, m;
char str[N];
cin >> n >> m >> str + 1;
p[0] = 1; // P^0 = 1
for (int i = 1; i <= n; i++) {
// 预处理 P^n
p[i] = p[i - 1] * P;
// str[i] 可为任意非0值
h[i] = h[i - 1] * P + str[i];
}
int l1, l2, r1, r2;
while (m--) {
cin >> l1 >> r1 >> l2 >> r2;
if (get(l1, r1) == get(l2, r2)) puts("Yes");
else puts("No");
}
return 0;
}
|
Trie 树
Trie树 用于高效存储和查找字符串集合
树节点为字母 例题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
const int N = 1e5 + 10; // 所有输入的字符串总长度不超过 10^5
int son[N][26], cnt[N], idx; // 根节点和空节点下标都是 0
// 插入字符串
void insert(string s) {
int p = 0; // 树的节点下标
for (int i = 0; s[i]; i++) {
int u = s[i] - 'a';
if (son[p][u] == 0) son[p][u] = ++idx;
p = son[p][u]; // 迭代向下
}
cnt[p]++;
}
// 查询字符串出现次数
int query(string s) {
int p = 0;
for (int i = 0; s[i]; i++) {
int u = s[i] - 'a';
if (son[p][u] == 0) return 0;
p = son[p][u];
}
return cnt[p];
}
|
树节点为数字 例题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
const int N = 1e5+10, M = N * 31; // M 节点个数 1e5 * 31
int son[M][2], idx; // 根节点和空节点都是 0
int a[N];
// 按位插入数字,其中 x 有效31位
void insert(int x) {
int p = 0;
for (int i = 30; i >= 0; i--) {
int t = (x >> i) & 1;
if (son[p][t] == 0) son[p][t] = ++idx;
p = son[p][t];
}
}
// 求与 x 异或最大的值(贪心)
int query(int x) {
int p = 0, res = 0;
for (int i = 30; i >= 0; i--) {
int t = (x >> i) & 1;
if (son[p][!t] != 0) {
res = res * 2 + 1;
p = son[p][!t];
} else {
res = res * 2;
p = son[p][t];
}
}
return res;
}
|
Trie 的结构体写法,速度上会慢一些,注意 query() 中的 res 更新使用了新的方法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
const int N = 1e5+10, M = N * 31;
int a[N];
struct Node {
Node *next[2];
// bool tag;
Node () {
memset(next, NULL, sizeof next);
// tag = false;
}
};
void insert(int x, Node *root) {
Node *p = root;
for (int i = 30; i >= 0; i--) {
int t = (x >> i) & 1;
if (p->next[t] == NULL) p->next[t] = new Node();
p = p->next[t];
}
}
// 求与 x 异或最大的值(贪心)
int query(int x, Node *root) {
Node *p = root;
int res = 0;
for (int i = 30; i >= 0; i--) {
int t = (x >> i) & 1;
if (p->next[!t] != NULL) {
res = res + (1 << i);
p = p->next[!t];
} else {
p = p->next[t];
}
}
return res;
}
// main
Node* root = new Node();
insert(a[i], root);
query(a[i], root);
|
并查集
并查集解决的问题:
- 合并集合
- 判断两元素是否在同一个集合
代码实现上注意两个细节:
- 路径压缩
p[x] = p[p[x]] => find() 中实现,常用
- 重量平衡,小树挂在大树下 =>
union() 中实现,一般不用
最 NB 的模板如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
const int N = 100010;
int p[N]; // 父指针数组
int cnt[N]; // 只保证根节点的 cnt 有意义
// 找根节点 同时 压缩路径(递归)
int Find(int x){
if (p[x] != x) p[x] = Find(p[x]);
return p[x];
}
// 合并集合(不考虑 cnt)
void Union1(int a, int b) {
p[Find(a)] = Find(b);
}
// 合并集合(考虑 cnt)
void Union2(int a, int b) {
int x = Find(a), y = Find(b);
if (x == y) return; // 已经在一个集合内,需要特判,否则 cnt 出错
p[x] = y;
cnt[y] += cnt[x];
}
// 初始化
for (int i = 0; i < N; i++) {
p[i] = i;
cnt[i] = 1;
}
|
Union() 考虑树的大小
1
2
3
4
5
6
7
8
9
10
11
|
void doUnion(int p, int q) {
int x = doFind(p), y = doFind(q);
if (x == y) return;
if (cnt[x] > cnt[y]) { // x 为大树,y 加入 x
p[y] = x;
cnt[x] += cnt[y];
} else {
p[x] = y;
cnt[y] += cnt[x];
}
}
|
Find() 其他写法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
int doFind1(int x) {
while (p[x] != x) {
p[x] = p[p[x]]; //路径压缩
x = p[x];
}
return x;
}
int doFind2(int x){
int a = x;
while(father[x] != x){
x = father[x];
}
while(father[a] != a){
int z = father[a];
father[a] = x;
a = z;
}
return x;
}
|
树状数组
前缀和数组可以快速 $O(1)$ 求出区间和,但当元素更新时需要以 $O(n)$ 的效率重新维护前缀和数组,此时可以使用树状数组优化,同时实现前缀和查询和单点更新这两个操作。LeetCode-307. 区域和检索 - 数组可修改
树状数组,也称作“二叉索引树”(Binary Indexed Tree)或 Fenwick 树
树状数组原理笔记
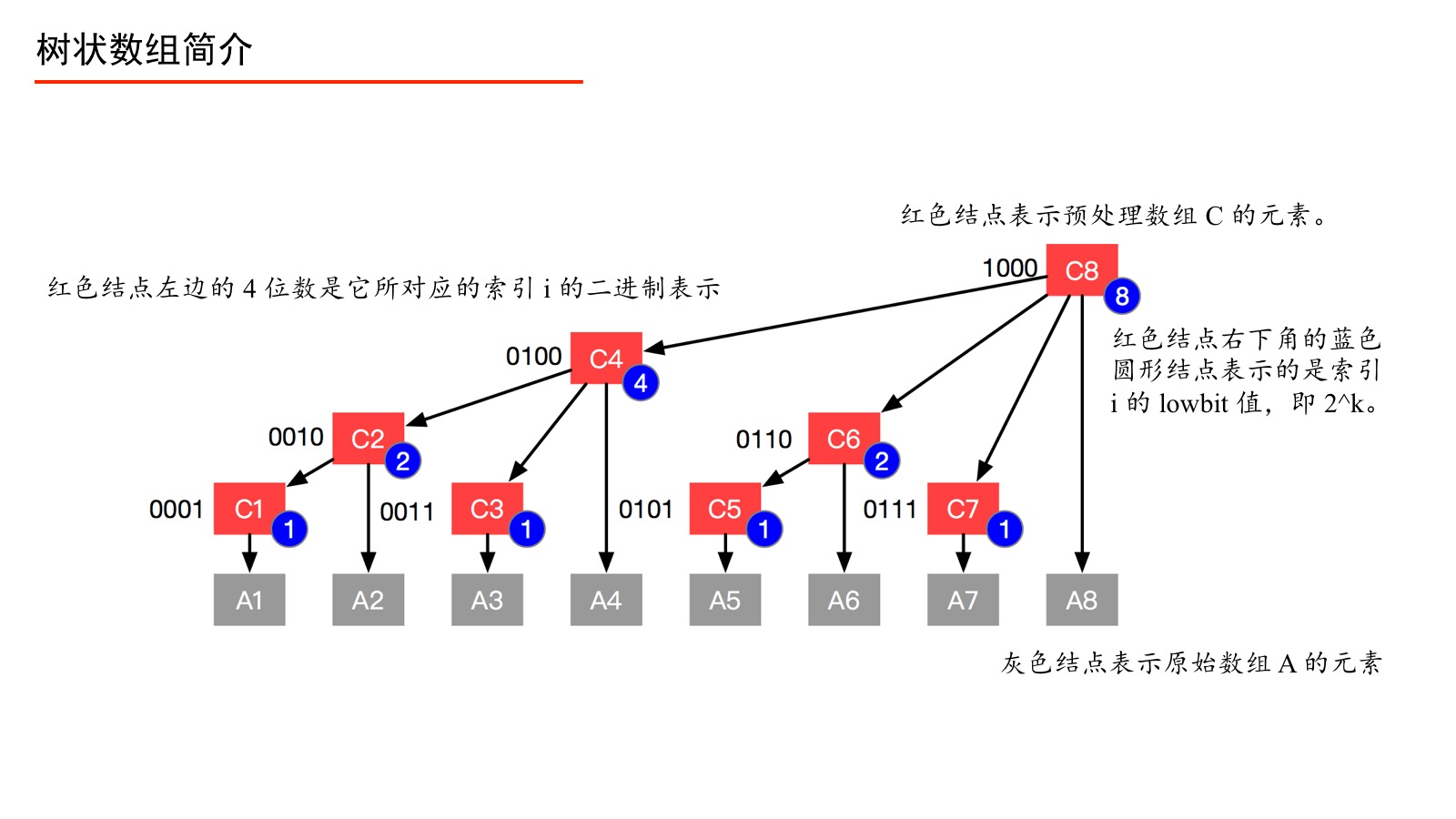
从已知子结点的索引 i,则结点 i 的父结点的索引 parent 的计算公式为:
$$parent(i)=i+lowbit(i)$$
代码模板如下(注意树状数组的下标一般从 1 开始):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
int lowbit(int x) {
return x & -x;
}
// 单点更新
void update(int x, int delta) {
for (int i = x; i <= len; i += lowbit(i)) {
tree[i] += delta;
}
}
// 求前缀和
int query_sum(int x) {
int sum = 0;
for (int i = x; i > 0; i -= lowbit(i)) {
sum += tree[i];
}
return sum;
}
|
初始化:树状数组的初始化可以通过单点更新来实现,因为最开始数组每个元素的值都为 0,每个都对应地加上原始数组的值,就完成了预处理数组 C 的创建
1
2
3
4
5
6
7
|
FenwickTree(vector<int>& nums) {
int n = nums.size();
vector<int> tree(n + 1);
for (int i = 0; i < n; i++) {
update(i + 1, nums[i]);
}
}
|
